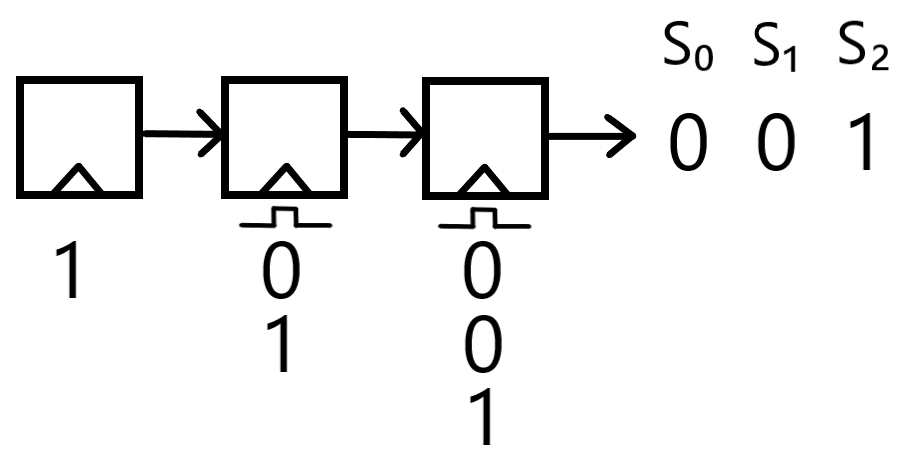
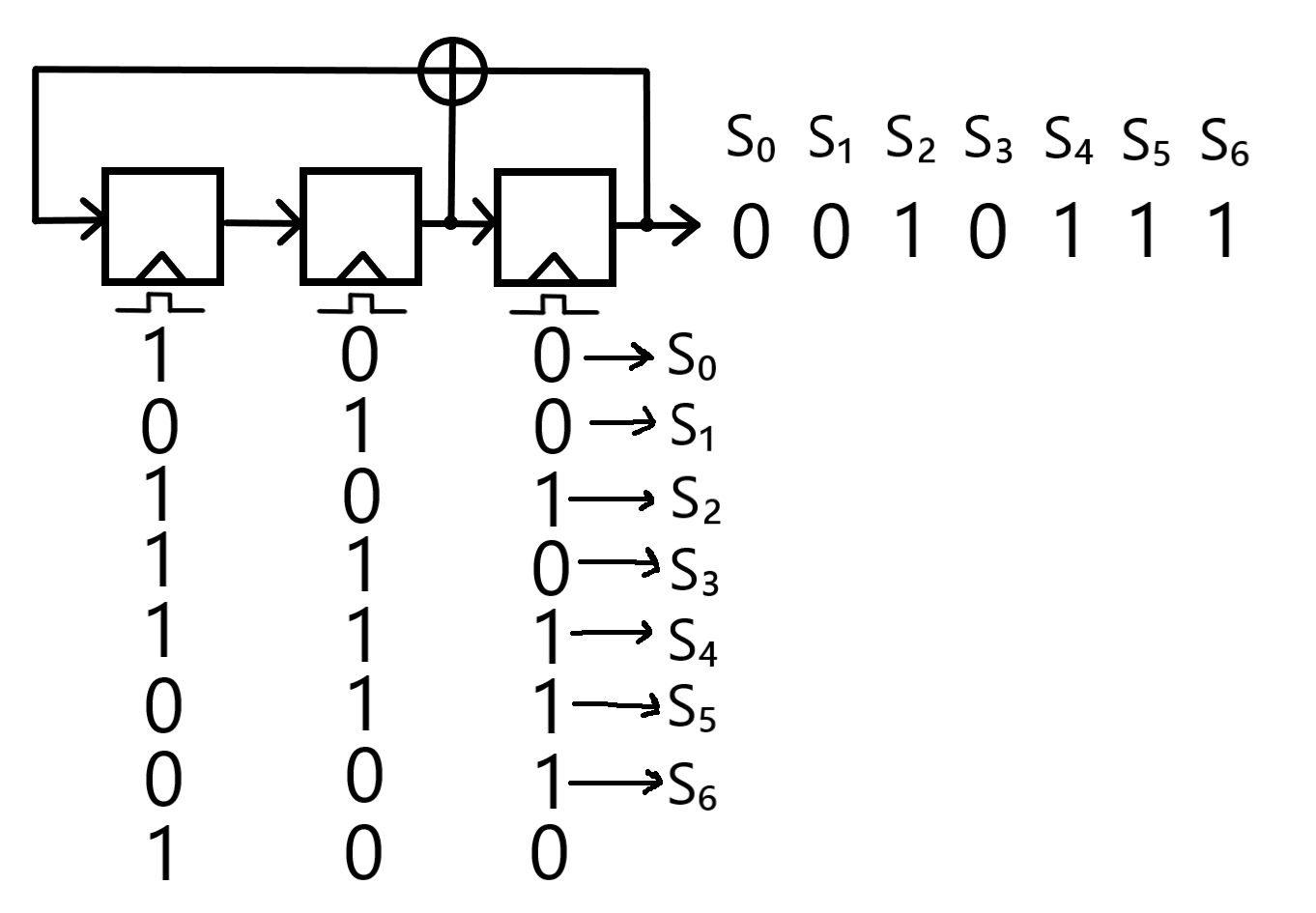
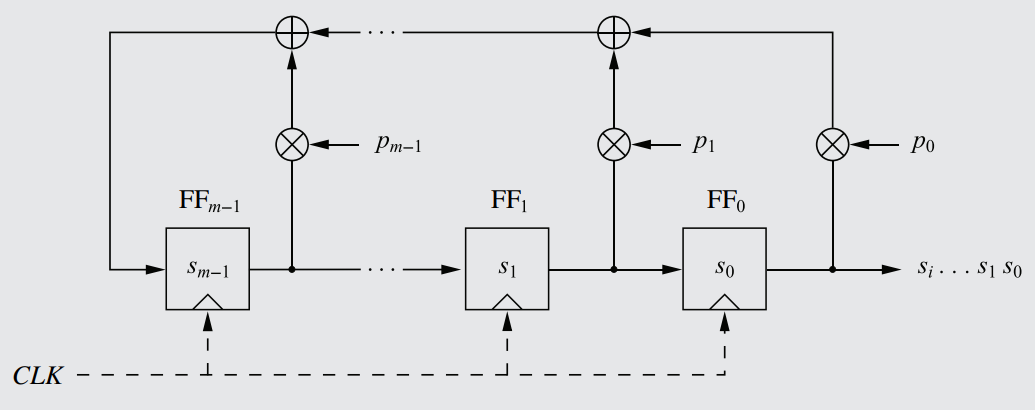
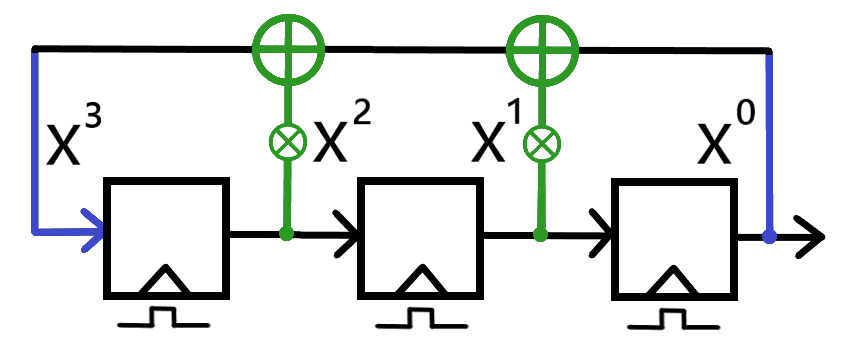
This is the first part of my complete notes for Symmetric Cryptography, covering such topics as Keystreams, Modular Arithmetic, Integer Rings, Shift Ciphers, Affine Ciphers, Stream Ciphers, Linear Feedback Shift Registers, and more.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Symmetric Cryptography, Part 1: Intro & Stream Ciphers.
Table Of Contents
I. Introductions
I.I Classification & Terminology.
# Fig. 1. - Cybersecurity Classification Hierarchy:
A Classification Hierarchy of the major components of Cryptology. For a further classification of Cryptanalysis, see Rule 7, and III.I for Symmetric Cryptography. The work of the mastermind Jonathan Lacabe himself.
# Cryptology/Cybersecurity: IT Security - the protection of digital information against misuse, incorporating technical, organizational, and implementation-specific aspects. This is the modern, digital theater of the much greater field of 'Security'.
All IT Security follows the CIA Triad: Confidentiality, Integrity and Availability of information. Security is largely focused on protecting against attackers, while system safety & reliability is focused on protecting against random technical failures.
# Cryptography: A sub-field of Cryptology;
The science of securing communication through encryption, especially against the cryptanalysis efforts of an adversary. Cryptographic algorithms are the bedrock of all cybersecurity systems - if cybersecurity is a car, then Cryptography is the engine.
# Cryptanalysis: A sub-field of Cryptology;
The reductive counterpart to Cryptography, the science of 'breaking' encryption and bypassing the cryptographic security. Though it is the medium of hackers and cybercriminals, it is also a serious scientific field for researchers to test the security of cryptosystems, i.e. systems established using Cryptography (see definition). This is the only to absolutely ensure the security of the cryptosystem - remember Schneier's Law.
# Cryptosystem: An application/implementation of a set of cryptographic algorithms (incorporating encryption, decryption, and other mechanisms).
# Symmetric Algorithms: A sub-field of Cryptography;
The classic form of Cryptography - two parties hold a secret key, enabling one party to encrypt a message and the other party to decrypt it. Thus, the same key is used for both encryption and decryption.
Until 1976, this was the only form of Cryptography in existence, and describes the basic nature of all historical ciphers (such as the shift/caesar cipher and affine cipher) and Stream Ciphers, Block Ciphers, and DES & AES. Although it is indeed the classic form of Cryptography, it is still highly relevant today, as AES remains an industry standard even into the quantum age.
Hash functions are somewhat similar to symmetric algorithms, though they can be considered an independent, third type of Cryptographic algorithm.
# Asymmetric/Public-Key Algorithms: A sub-field of Cryptography;
The great cryptographic breakthrough of the 20th century, Asymmetric Cryptography (a.k.a. "Public Key Cryptography") is the backbone of most modern cryptosystems and is what much of the infrastructure of the Internet (protocols, in particular) is based on.
Invented by the Diffie-Hellman team in 1976, Public-Key Cryptography functions by having each party have TWO keys, a private key and a public key.
For more detail on how these algorithms work, see the "Public-Key Cryptography" Subcategory ([[[[[), but know they are used in a variety of fashions: digital signatures, key establishment/management, and more!
# Protocols: A sub-field of Cryptography;
Collective cryptographic algorithms that serve a complex security function, like a library of algorithms that work together for a common goal. For example - the Transport Layer Security scheme (TLS) and the Hypertext Transfer Protocol (HTTP) are used in every web browser.
In the words of Edward Snowden, "[The Internet of Things and countless] protocols have given us the means to digitize and put online damn near everything in the world that we don’t eat, drink, wear, or dwell in."
#
C. Rule .
In Cryptography, 'Primitives', 'Ciphers', and 'Algorithms' all refer to different parts of the same process: the components of a cryptosystem at different scales, algorithms being the largest scale component and primitives being the smallest.
Primitives are the basic cryptographic functions (building blocks of an algorithm), Ciphers are the implementation of an encryption scheme, and Algorithms are the combined procedures of primitives and ciphers to create the greater cryptosystem.
For example, a well-formed algorithm may incorporate the AES cipher (see Rule [[[), which uses the key schedule primitive (see Rule 51) to assist in both encrypting and decrypting the data.
Primitives are the basic cryptographic functions (building blocks of an algorithm), Ciphers are the implementation of an encryption scheme, and Algorithms are the combined procedures of primitives and ciphers to create the greater cryptosystem.
For example, a well-formed algorithm may incorporate the AES cipher (see Rule [[[), which uses the key schedule primitive (see Rule 51) to assist in both encrypting and decrypting the data.
# Channel: A transmission medium for data to pass through. Examples include the Internet, airways, and Wi-Fi. Securing transmitted data from being intercepted, and from being intercepted in any meaningful form, is the goal of Cryptography.
# Hybrid Schemes: The combined usage of both asymmetric and symmetric algorithms in a cryptosystem, since both types have their own strengths and weaknesses (See [[[).
I.II Symmetric Crypto. Basics.
#
C. Rule .
Symmetric Cryptosystem:
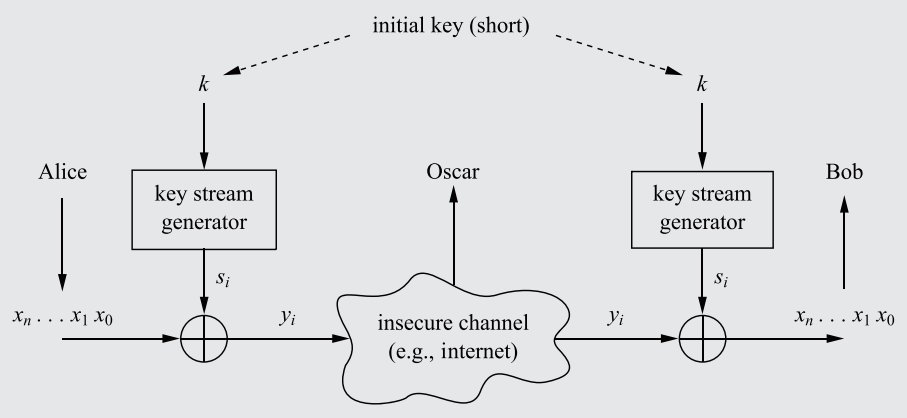
The ancient problem presents itself: How can two parties communicate over an insecure channel (an 'open channel') without having their communications intercepted by a third-party?
Say Alice and Bob connect through the internet (which is an open channel due to the potential of package rerouting/interception) and transfer data. An opponent, Oscar, can read their communications by intercepting the data before it reaches Bob.
A diagram showcasing how communications between Alice and Bob, when passing through an insecure channel unencrypted, can be intercepted by the attacker Oscar.
To stop Oscar from reading the message, an encryption algorithm can be established, converting the plaintext message (x) into a ciphertext message (y), and then sending it through the insecure channel. Oscar would only see a stream of random characters/bits as a result of the encryption. Bob, using a decryption function, would convert the ciphertext back into plaintext, thus completing the data transfer without interception.
In order for Bob to not simply decrypt the ciphertext immediately using the decryption function (which, counterintuitively, should actually be made publicly available - see Rule 3), a Key only known to Alice and Bob (sent through a secure, impenetrable channel) must be used as a parameter in both the encryption and decryption functions.
The key must be inputted into the encryption function to influence the manner in which the plaintext is encrypted into cyphertext. Thus, only with the key will Bob be able to decrypt the Ciphertext. Oscar, who doesn't know the key, will be unable to decrypt the message, even if the decryption algorithm is public.
A diagram showcasing a symmetric cryptosystem, complete with a key sent through a secure channel and encryption/decryption functions.
x = Plaintext message - the unadulterated, original content of the message.
y = Ciphertext, which looks like scrambled characters to an interceptor like Oscar.
e = Encryption function, a mathematical formula that converts x into y.
d = Decryption function, a mathematical formula that converts y into x.
K = The Key fed into the encryption and decryption functions.
|K|, 𝒦 = Keyspace, the total number of possible keys in a cryptosystem. This matters significantly with regard to brute-force Cryptanalysis (see Rule 8), and entails other characteristics detailed in Rule 6.
The ancient problem presents itself: How can two parties communicate over an insecure channel (an 'open channel') without having their communications intercepted by a third-party?
Say Alice and Bob connect through the internet (which is an open channel due to the potential of package rerouting/interception) and transfer data. An opponent, Oscar, can read their communications by intercepting the data before it reaches Bob.
A diagram showcasing how communications between Alice and Bob, when passing through an insecure channel unencrypted, can be intercepted by the attacker Oscar.
To stop Oscar from reading the message, an encryption algorithm can be established, converting the plaintext message (x) into a ciphertext message (y), and then sending it through the insecure channel. Oscar would only see a stream of random characters/bits as a result of the encryption. Bob, using a decryption function, would convert the ciphertext back into plaintext, thus completing the data transfer without interception.
In order for Bob to not simply decrypt the ciphertext immediately using the decryption function (which, counterintuitively, should actually be made publicly available - see Rule 3), a Key only known to Alice and Bob (sent through a secure, impenetrable channel) must be used as a parameter in both the encryption and decryption functions.
The key must be inputted into the encryption function to influence the manner in which the plaintext is encrypted into cyphertext. Thus, only with the key will Bob be able to decrypt the Ciphertext. Oscar, who doesn't know the key, will be unable to decrypt the message, even if the decryption algorithm is public.
A diagram showcasing a symmetric cryptosystem, complete with a key sent through a secure channel and encryption/decryption functions.
x = Plaintext message - the unadulterated, original content of the message.
y = Ciphertext, which looks like scrambled characters to an interceptor like Oscar.
e = Encryption function, a mathematical formula that converts x into y.
d = Decryption function, a mathematical formula that converts y into x.
K = The Key fed into the encryption and decryption functions.
|K|, 𝒦 = Keyspace, the total number of possible keys in a cryptosystem. This matters significantly with regard to brute-force Cryptanalysis (see Rule 8), and entails other characteristics detailed in Rule 6.
#
C. Rule .
Keeping the encryption/decryption algorithms 'e' and 'd' secret, preventing their cryptanalysis by the enemy (known as Security by Obscurity), was standard procedure for the ~4000 year history of Cryptography prior to the discovery of public-key Cryptography. However, the only way of ensuring the security of the algorithms is to make them public so that they can be analyzed by cryptanalysts.
This is the central principle of a foundational law in Cryptography, postulated in 1883 by Auguste Kerckhoffs:
Kerckhoffs' Principle:
"A cryptosystem should be secure even if the attacker (Oscar) knows all the details of the system, with the exception of the secret key."
In Practice: Never use an untested Crypto algorithm! Furthermore, never roll your own crypto!
This is the central principle of a foundational law in Cryptography, postulated in 1883 by Auguste Kerckhoffs:
Kerckhoffs' Principle:
"A cryptosystem should be secure even if the attacker (Oscar) knows all the details of the system, with the exception of the secret key."
In Practice: Never use an untested Crypto algorithm! Furthermore, never roll your own crypto!
# End-To-End Encryption (E2EE): A system of encryption widely used in modern communication services (like internet messaging sites), in which all data sent from Alice to Bob (party #1 to party #2) is never decrypted at any point along its route until it reaches Bob.
Thus, all parties intercepting/eavesdropping will be unable to read or manipulate the message, even if they control any of the base stations the message goes through.
An example of how communications between Alice and Bob would occur under a end-to-end encryption scheme.
I.III Key Terminology.
Binary is a crucial element of how most (and practically all modern) cryptosystems work, and several phrases commonly used in cryptographic discussions directly reference this inherent nature. As such, let it be known: all references to 'bits' of any kind are made in regard to 1s and 0s.
#
C. Rule .
Bit-Length:
Mathematical Definition:
Value-based Bit-length = ⌊log2 N⌋ + 1
Set-based Bit-length = ⌈log2 S⌉
N = Any given number.
S = Any given set.
⌊, ⌋ = The Floor function, which returns the greatest integer less than or equal to the given value.
⌈, ⌉ = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Bit-length is a mathematical term with two definitions and two associated equations, the application of which depends on the context of what you are trying to find the bit-length of. Apart from being able to determine when to apply either definition, bit-length is a remarkably simple concept that hinges on comprehension of binary.
The first definition is value-based, while the second is set-based.
The bit-length of a value is the # of bits required to represent a given number.
The bit-length of a set is the # of bits necessary to represent the number of values within the set.
While the value-based definition is most popular in computer science (such as in the bit_length() method in Python), the set-based definition is the most popular and relevant in Cryptography. Thus, in cryptographic discussions, it is practically always safe to assume that the term 'bit-length' is being used in regard to the set-based definition.
As such, two distinct equations emerge to represent these binary operations. As shown in the mathematical definition, the value-based bit-length uses the floor function while the set-based bit-length uses the ceiling function, rounding downward and upward for any decimal value, respectively.
For an example of the two in practice, a keyspace of 2^3 (8 values) would have a value-based bit-length of 4, since 8 is 1000 in binary, and would have a set-based bit-length of 3, since exactly 3 bits would be required to account for every value within the keyspace: 000 through 111 represent a total of 8 values, reaching a highest value of 𝒦-1.
With regards to set-based bit-length, this does not mean that each individual value requires three bits to represent it; the value of 1 only "requires" 1 bit to represent it, for example. The set-based bit-length only really means the total number of bits necessary to represent 𝒦-1, which thus accounts for all of the values before it (through the nature of binary representation).
Mathematical Definition:
Value-based Bit-length = ⌊log2 N⌋ + 1
Set-based Bit-length = ⌈log2 S⌉
N = Any given number.
S = Any given set.
⌊, ⌋ = The Floor function, which returns the greatest integer less than or equal to the given value.
⌈, ⌉ = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Bit-length is a mathematical term with two definitions and two associated equations, the application of which depends on the context of what you are trying to find the bit-length of. Apart from being able to determine when to apply either definition, bit-length is a remarkably simple concept that hinges on comprehension of binary.
The first definition is value-based, while the second is set-based.
The bit-length of a value is the # of bits required to represent a given number.
The bit-length of a set is the # of bits necessary to represent the number of values within the set.
While the value-based definition is most popular in computer science (such as in the bit_length() method in Python), the set-based definition is the most popular and relevant in Cryptography. Thus, in cryptographic discussions, it is practically always safe to assume that the term 'bit-length' is being used in regard to the set-based definition.
As such, two distinct equations emerge to represent these binary operations. As shown in the mathematical definition, the value-based bit-length uses the floor function while the set-based bit-length uses the ceiling function, rounding downward and upward for any decimal value, respectively.
For an example of the two in practice, a keyspace of 2^3 (8 values) would have a value-based bit-length of 4, since 8 is 1000 in binary, and would have a set-based bit-length of 3, since exactly 3 bits would be required to account for every value within the keyspace: 000 through 111 represent a total of 8 values, reaching a highest value of 𝒦-1.
With regards to set-based bit-length, this does not mean that each individual value requires three bits to represent it; the value of 1 only "requires" 1 bit to represent it, for example. The set-based bit-length only really means the total number of bits necessary to represent 𝒦-1, which thus accounts for all of the values before it (through the nature of binary representation).
#
C. Rule .
Key-Length:
Mathematical Definition:
Key-length = ⌈log2 𝒦⌉
𝒦 = Keyspace, the total number of possible keys in a cryptosystem.
⌈, ⌉ = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Key-Length is a concept that builds upon the idea of bit-length, which is explained in Rule 4. Comprehension of bit-length (and the different between value-based and set-based bit-length) is prerequisite for understanding key-length.
In its essence, Key-length is a narrowed application of set-based bit-length specific to the bit-length of the key of a cryptosystem. It is identical in every way to the set-based bit-length definition, except for the minute change of "set" to "keyspace":
The bit-length of a keyspace is the # of bits necessary to represent the number of values within the keyspace. This value is known as the key-length.
Set-based bit-length, and its particular use-case of key-length, will appear with some ubiquity in the Cryptographic Summary. Note how key-length is basically just a subtype of bit-length, just like how keybits (see definition) are a more specific type of bit. However, they can NOT be used interchangeably, for reasons outlined below.
In Cryptography, the key-length is only relevant/existent if the cryptosystem uses binary representation, as detailed in Rule 6. The number of bits necessary to represent each value of the keyspace is meaningless if there are no 'bits' involved in the cryptosystem, as is the case for the Shift Cipher (Rule 20), which has a keyspace of 26 but no meaningful key-length. Somewhat ironically, bit-length does not require a bit-based system to have a meaningful result, as it merely denotes the process of converting a value to its binary form.
Mathematical Definition:
Key-length = ⌈log2 𝒦⌉
𝒦 = Keyspace, the total number of possible keys in a cryptosystem.
⌈, ⌉ = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Key-Length is a concept that builds upon the idea of bit-length, which is explained in Rule 4. Comprehension of bit-length (and the different between value-based and set-based bit-length) is prerequisite for understanding key-length.
In its essence, Key-length is a narrowed application of set-based bit-length specific to the bit-length of the key of a cryptosystem. It is identical in every way to the set-based bit-length definition, except for the minute change of "set" to "keyspace":
The bit-length of a keyspace is the # of bits necessary to represent the number of values within the keyspace. This value is known as the key-length.
Set-based bit-length, and its particular use-case of key-length, will appear with some ubiquity in the Cryptographic Summary. Note how key-length is basically just a subtype of bit-length, just like how keybits (see definition) are a more specific type of bit. However, they can NOT be used interchangeably, for reasons outlined below.
In Cryptography, the key-length is only relevant/existent if the cryptosystem uses binary representation, as detailed in Rule 6. The number of bits necessary to represent each value of the keyspace is meaningless if there are no 'bits' involved in the cryptosystem, as is the case for the Shift Cipher (Rule 20), which has a keyspace of 26 but no meaningful key-length. Somewhat ironically, bit-length does not require a bit-based system to have a meaningful result, as it merely denotes the process of converting a value to its binary form.
# Keybits: The binary bits in the key used in a cryptosystem. A key-length, for example, is composed of keybits. In Cryptography, a "256-keybit key-length" is regarded as secure against brute-force attacks (see Rule 8).
# Bits of Entropy/Key Entropy: A term frequently used in cryptography, essentially just meaning a number that represents the degree of security a cryptosystem has with respect to its keyspace. It has the equation ⌈log2 𝒦⌉, where 𝒦 is the keyspace of a cryptosystem (the number of possible keys). For example, if a cryptosystem has 2^100 keys, then that cryptosystem has 100 bits of entropy.
It really is just a term used to flex security against brute-force attacks (Rule 8), not in reference to anything tangible other than the size of the keyspace itself - it is a self-referential term, actively disguising useful information behind additional artificial buzzwords.
It happens to share the same equation as the key-length (as detailed in Rule 6 below), but note that "bits of entropy" is not a term chained to any particular requirement and can thus be applied to any cryptosystem, while the concept of a key-length has several prerequisites that limit its usage. This is in spite of the fact that "bits of entropy" uses the word "bit" - it, like bit-length (but unlike key-length, as distinguished in Rule 5), can be reasonably applied in non-bit-based cryptosystems.
#
C. Rule .
Keyspace Mathematics:
In Symmetric Cryptography, there is an inherent relation between the keyspace of a cryptosystem (|K| or 𝒦), and the key-length of the key (L) that the cryptosystem uses (which is dealt with in detail in Rule 5). It is fairly simple and intuitive, but has some key caveats.
If the algorithm uses a 168-bit key, then there are 2^168 possible keys. This is because the keyspace is the number of possible values that could be represented by the bits of the key-length - a key-length of 5 would have 32 possible values, i.e. every value between 00000 and 11111. Mathematically, this is represented using either of the following equations:
𝒦 = 2ᴸ
L = ⌈log2 𝒦⌉
These two equations are equivalent, with the second one derived by taking the log of both sides of the first (uncoincidentally forming the key-length equation as described in Rule 5). The ceiling function (which rounds to the closest greater number) is applied to the logarithm to ensure that the key-length is an integer. Of course, the relation only holds insofar that all keys of length L are valid and equally likely to occur, which rules out any symmetric cryptosystem with selective application of its keys/keybits.
There are some limitations that narrow the applicability of this relation - in effect, it only really applies to modern symmetric cryptosystems (unless specified otherwise, like the aforementioned DES). First, all ciphers that do not explicitly have a key-length, such as those that operate on letters instead of bits (e.g., every historical cipher in Section II), do not qualify. A cipher must structure its keys in the form of binary strings with fixed lengths in order for the relation to be applicable.
As stated in its definition, the very concept of a "keybit" is dependent on the fact that the cipher is using a key made from binary bits - any ciphers that do not meet that requirement are instantly null in regards to the given relation.
For example, the Shift Cipher (see Rule 20) has a keyspace of 26, but that in no way means that the "key-length" of the cipher is log2 26 (though it will indeed have log2 26 "bits of entropy"). For non-bit cryptosystems, there is no real key-length, but these ciphers are outdated nonsense cryptography that are not to be taken seriously anyways.
Furthermore, this relation does not hold for asymmetric cryptography: There is a significant difference between symmetric keys and asymmetric keys: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key. For information as to why this is, see Rule [[[.
In Symmetric Cryptography, there is an inherent relation between the keyspace of a cryptosystem (|K| or 𝒦), and the key-length of the key (L) that the cryptosystem uses (which is dealt with in detail in Rule 5). It is fairly simple and intuitive, but has some key caveats.
If the algorithm uses a 168-bit key, then there are 2^168 possible keys. This is because the keyspace is the number of possible values that could be represented by the bits of the key-length - a key-length of 5 would have 32 possible values, i.e. every value between 00000 and 11111. Mathematically, this is represented using either of the following equations:
𝒦 = 2ᴸ
L = ⌈log2 𝒦⌉
These two equations are equivalent, with the second one derived by taking the log of both sides of the first (uncoincidentally forming the key-length equation as described in Rule 5). The ceiling function (which rounds to the closest greater number) is applied to the logarithm to ensure that the key-length is an integer. Of course, the relation only holds insofar that all keys of length L are valid and equally likely to occur, which rules out any symmetric cryptosystem with selective application of its keys/keybits.
There are some limitations that narrow the applicability of this relation - in effect, it only really applies to modern symmetric cryptosystems (unless specified otherwise, like the aforementioned DES). First, all ciphers that do not explicitly have a key-length, such as those that operate on letters instead of bits (e.g., every historical cipher in Section II), do not qualify. A cipher must structure its keys in the form of binary strings with fixed lengths in order for the relation to be applicable.
As stated in its definition, the very concept of a "keybit" is dependent on the fact that the cipher is using a key made from binary bits - any ciphers that do not meet that requirement are instantly null in regards to the given relation.
For example, the Shift Cipher (see Rule 20) has a keyspace of 26, but that in no way means that the "key-length" of the cipher is log2 26 (though it will indeed have log2 26 "bits of entropy"). For non-bit cryptosystems, there is no real key-length, but these ciphers are outdated nonsense cryptography that are not to be taken seriously anyways.
Furthermore, this relation does not hold for asymmetric cryptography: There is a significant difference between symmetric keys and asymmetric keys: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key. For information as to why this is, see Rule [[[.
I.IV Cryptanalysis Basics.
A Classification hierarchy of Cryptanalysis. There are two main branches of Classical Cryptanalysis, Brute-force and Analytical Cryptanalysis. See Subsection I.I for the full classification and III.I for Symmetric Cryptography.
#
C. Rule .
There are multitudes of cryptanalysis techniques, and the crucial law is that if just one attack works, then the entire cryptosystem crumbles and fails, regardless of how secure it is against other attack types.
For example, while a substitution cipher (see Rule 10) may be impenetrable to a brute-force attack (Rule 8) with its 2^88 keyspace, it collapses against letter frequency analysis (also described in Rule 10).
In order for a cryptosystem to be considered secure, it must be resistant against every single type of attack. An attacker always looks for the weakest link in the cryptosystem. Thus, in addition to strong algorithms, safeguards against social engineering and implementation attacks (see definitions below) must be instituted.
For example, while a substitution cipher (see Rule 10) may be impenetrable to a brute-force attack (Rule 8) with its 2^88 keyspace, it collapses against letter frequency analysis (also described in Rule 10).
In order for a cryptosystem to be considered secure, it must be resistant against every single type of attack. An attacker always looks for the weakest link in the cryptosystem. Thus, in addition to strong algorithms, safeguards against social engineering and implementation attacks (see definitions below) must be instituted.
# Classical Cryptanalysis: A sub-field of Cryptanalysis (see Fig. 2);
The basic, algorithm-focused approach to cryptanalysis in which you analyze the inputs and outputs to probe a viable attack vector. This is the "real" cryptanalysis in the eyes of the cryptography snobs, in which you try to poke holes in the design of the cryptosystem itself.
# Social Engineering: A sub-field of Cryptanalysis (see Fig. 2);
The process of bypassing the protections of a cryptosystem by going directly after the humans that have access to the secret key. Obtaining the key can range from kidnapping and forcing them to tell the key/password, to a simple phishing scheme over the phone or through email.
# Implementation Attacks: A sub-field of Cryptanalysis (see Fig. 2);
Extraction of the key through 'side-channel analysis'. By observing the behavior of the implementation of the cryptosystem in an IC or software, it is possible to deduce important information relating to the key.
For example: By looking at the electrical power consumption or electromagnetic radiation of a CPU running a cryptographic algorithm, a signal processing technique can be used to recover the key (see E.E. [[[[[). The runtime behavior can also indicate information regarding the key, which is why many cryptographers ensure constant runtimes in embedded cryptosystems.
These attacks are most relevant when the attacker has physical access to a piece of hardware running the cryptosystem, such as a credit card.
# Attack Vectors: The many possible ways to attack a cryptosystem; the types of cryptanalysis that can be used, including (but not limited to) those shown in Fig. 2.
# Moore’s Law: The computing power of the strongest computers (e.g., the number of transistors in an integrated circuit) will double every 18-24 months while the price will remain constant. This means that computing power, growing exponentially over time, will continually pose more and more of a threat to modern cryptographic systems and to antiquated ones still in use, as it becomes cheaper and faster to break them.
This is especially relevant for cryptanalysis requiring intensive computing power, such as brute-force attacks (see Rule 8 below). See Rule 55 for an example of how Moore's Law made feasible a brute-force attack on a keylength that was previously considered secure against keysearch attacks.
#
C. Rule .
Classical Attack #1: Brute-Force Attack/Exhaustive Key search:
Mathematical Definition:
Let (x, y) denote the pair of plaintext and ciphertext, and let K = {k1 ,..., kκ} be the keyspace of all possible keys ki. A brute-force attack now checks for every ki ∈ K whether dki == x.
If the equality holds, a possible correct key is found; if not, proceed with the next key.
Explanation:
The testing of all possible keys in a given keyspace with the decryption function, to find the key that will produce the plaintext. This is akin to thinking of the cryptosystem as a black box, in which the only significant factor to decoding an encrypted message is the number of possible keys the message could have been created with.
As shown in the illustration below, different keyspaces take different amounts of time to crack using brute-force. As such, only algorithms with a sufficiently large keyspace can be considered secure against brute-force, though not necessarily against any other form of attack.
A chart of the time it would take to crack keyspaces of various lengths using a brute-force attack.
As of 2024, the largest keyspace that can be searched in a relatively reasonable amount of time is 2^80. However, not all keybits are created equally: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key, as noted in Rule 6. For why this is, see Rule [[[.
Mathematical Definition:
Let (x, y) denote the pair of plaintext and ciphertext, and let K = {k1 ,..., kκ} be the keyspace of all possible keys ki. A brute-force attack now checks for every ki ∈ K whether dki == x.
If the equality holds, a possible correct key is found; if not, proceed with the next key.
Explanation:
The testing of all possible keys in a given keyspace with the decryption function, to find the key that will produce the plaintext. This is akin to thinking of the cryptosystem as a black box, in which the only significant factor to decoding an encrypted message is the number of possible keys the message could have been created with.
As shown in the illustration below, different keyspaces take different amounts of time to crack using brute-force. As such, only algorithms with a sufficiently large keyspace can be considered secure against brute-force, though not necessarily against any other form of attack.
A chart of the time it would take to crack keyspaces of various lengths using a brute-force attack.
As of 2024, the largest keyspace that can be searched in a relatively reasonable amount of time is 2^80. However, not all keybits are created equally: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key, as noted in Rule 6. For why this is, see Rule [[[.
#
C. Rule .
Classical Attack #2: Analytical Attacks:
The intelligent counterpart to 'brute'-force, Analytical Attacks examine the internal characteristics of the encryption function and pick apart weaknesses that could enable reconstruction of the plaintext message, such as Letter Frequency Analysis (for the Substitution Cipher, see Rule 10) and Differential Cryptanalysis (for Block and Stream Ciphers, see Rule [[[[).
There is no 'equation' for Analytical Attacks, because they are specific and unique to every cryptosystem (though some common characteristics can emerge between similar cryptosystems).
The intelligent counterpart to 'brute'-force, Analytical Attacks examine the internal characteristics of the encryption function and pick apart weaknesses that could enable reconstruction of the plaintext message, such as Letter Frequency Analysis (for the Substitution Cipher, see Rule 10) and Differential Cryptanalysis (for Block and Stream Ciphers, see Rule [[[[).
There is no 'equation' for Analytical Attacks, because they are specific and unique to every cryptosystem (though some common characteristics can emerge between similar cryptosystems).
I.V Generic Analytical Attacks.
# Ciphertext-only Attack: An attack in which the adversary only has knows the ciphertext.
# Known-plaintext Attack: In addition to the ciphertext, the adversary also knows some pieces of the plaintext (e.g., header information of an encrypted file or email).
# Chosen-plaintext Attack: An attack in which the adversary can choose the plaintext that is being encrypted and also has access to the corresponding ciphertext, found through possession of the decryption function (whether the attacker is aware of its internal workings or not). This attack is primarily used to find a key that is being reused in a communication, so that further ciphertexts encrypted with the key can be decrypted.
# Chosen-ciphertext Attack: An attack in which the adversary can choose ciphertexts and obtain the corresponding plaintexts, the goal being (typically) to recover the secret key.
II. Historical Ciphers & Modular Arithmetic.
II.I Substitution Cipher.
Because these ciphers do not operate on bits (and thus do not have keys structured in the form of binary strings with fixed lengths), the relation between keyspace and keybit-length as detailed in Rule 6 does not apply to these ciphers does not apply to these ciphers.
#
C. Rule .
Substitution Cipher
A historical cipher, operating purely on letters, in which every plaintext letter is replaced by a fixed ciphertext letter. It is just scrambling the letters, nothing more.
The Keyspace is 26!, or 2^88, as each plaintext letter that maps to a ciphertext letter decreases the remaining number of possible letters. Thus, a brute-force attack would be out of the question for modern computers.
Since the different letters of the English alphabet have different frequencies of appearance (see the image below), and these frequencies are preserved even after scrambling (just different letters will have the frequencies), Letter Frequency Analysis can be conducted as an attack on the substitution cipher, making cracking the cipher rather simple.
This is an example of a cipher/algorithm in which an Analytical Attack (see Rule 9) is most effective.
A generalized distribution of letters in the english language. In substitution ciphers, the frequencies remain the same, with only the letters that represent them changing. Courtesy of Wikimedia.
A historical cipher, operating purely on letters, in which every plaintext letter is replaced by a fixed ciphertext letter. It is just scrambling the letters, nothing more.
The Keyspace is 26!, or 2^88, as each plaintext letter that maps to a ciphertext letter decreases the remaining number of possible letters. Thus, a brute-force attack would be out of the question for modern computers.
Since the different letters of the English alphabet have different frequencies of appearance (see the image below), and these frequencies are preserved even after scrambling (just different letters will have the frequencies), Letter Frequency Analysis can be conducted as an attack on the substitution cipher, making cracking the cipher rather simple.
This is an example of a cipher/algorithm in which an Analytical Attack (see Rule 9) is most effective.
A generalized distribution of letters in the english language. In substitution ciphers, the frequencies remain the same, with only the letters that represent them changing. Courtesy of Wikimedia.
II.II Modular Arithmetic Basics.
#
C. Rule .
Modular Arithmetic:
Mathematical Definition:
(a, r, m) ∈ ℤ
m > 0
If m|(a − r), then a ≡ r mod m
ℤ = The set of all integers.
a = The chosen number.
r = The remainder.
m = The modulus, the highest possible number in the set.
'mod m' = The modulus operator / remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to m.
Explanation:
Since the bulk of cryptographic computations are performed in finite sets, special mathematical tools are needed. In particular, Modular Arithmetic is the basis for all modern cryptosystems, and many historical ones as well.
Modular arithmetic is a system of simplifying a number in terms of a given modulus, the highest number in a set. As shown in the mathematical definition, any chosen number greater than the modulus is rewritten using the modulus operator (a.k.a. the remainder operator) with respect to the difference between the number and any multiple (see Rule 12) of the modulus, known as the remainder.
The best example for understanding modular arithmetic is something most are already familiar with: time on a clock. On clocks, the highest number is 12, and going any higher just loops back to the beginning. In effect, a clock is a modular arithmetic system using a set of {1, 2, ... 12} with a modulus of 12. 13 hours, for example, would be represented as 1 mod 12, using the modulus operator as specified in the mathematical definition.
The process of finding the modular equivalent of a number (in relation to an already known modulus/set) is simple: divide the chosen number by the modulus, and find the remainder (see Rule 12). The remainder will then be placed as the coefficient in front of the modulus operator. All numbers smaller than the modulus are rendered ordinarily, without the mod operator. For example, the modular representation of 4 in the clock example (mod 12) is just 4.
Using modular representation is a bit jarring at first, as it effectively 'wraps' the chosen number around the modulus, but frequent use (as it is used in practically every cryptosystem) will make it second nature to the beginning cryptographer.
Mathematical Definition:
(a, r, m) ∈ ℤ
m > 0
If m|(a − r), then a ≡ r mod m
ℤ = The set of all integers.
a = The chosen number.
r = The remainder.
m = The modulus, the highest possible number in the set.
'mod m' = The modulus operator / remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to m.
Explanation:
Since the bulk of cryptographic computations are performed in finite sets, special mathematical tools are needed. In particular, Modular Arithmetic is the basis for all modern cryptosystems, and many historical ones as well.
Modular arithmetic is a system of simplifying a number in terms of a given modulus, the highest number in a set. As shown in the mathematical definition, any chosen number greater than the modulus is rewritten using the modulus operator (a.k.a. the remainder operator) with respect to the difference between the number and any multiple (see Rule 12) of the modulus, known as the remainder.
The best example for understanding modular arithmetic is something most are already familiar with: time on a clock. On clocks, the highest number is 12, and going any higher just loops back to the beginning. In effect, a clock is a modular arithmetic system using a set of {1, 2, ... 12} with a modulus of 12. 13 hours, for example, would be represented as 1 mod 12, using the modulus operator as specified in the mathematical definition.
The process of finding the modular equivalent of a number (in relation to an already known modulus/set) is simple: divide the chosen number by the modulus, and find the remainder (see Rule 12). The remainder will then be placed as the coefficient in front of the modulus operator. All numbers smaller than the modulus are rendered ordinarily, without the mod operator. For example, the modular representation of 4 in the clock example (mod 12) is just 4.
Using modular representation is a bit jarring at first, as it effectively 'wraps' the chosen number around the modulus, but frequent use (as it is used in practically every cryptosystem) will make it second nature to the beginning cryptographer.
# Cyclic Shift/Cyclical Shift: A fancy term essentially just denoting the usage of modular arithmetic in a particular context, with sets wrapping around once they reach an overflow value and whatnot.
#
C. Rule .
Modular Arithmetic: Computation of the Remainder.
Mathematical Definition:
(a, m) ∈ ℤ
a = (q × m) + r
Thus, a - (q × m) = r
ℤ = The set of all integers.
a = The chosen number.
q = The quotient, which produces a multiple of the modulus.
r = The remainder.
m = The modulus, the highest possible number in the set.
Explanation:
To find the remainder in a modular arithmetic system (see Rule 11) when only the chosen number and the modulus (a and m) are known, there is an exact, algorithmic definition. Note that there are two unknown variables in this equation - the quotient and the remainder (q & r). As such, the quotient will have to be determined first in order to find the remainder.
Any integer will work for the quotient (as a result of equivalence classes, which will be discussed later in Rule 13), but the preferred quotient will be the one that produces the preferred multiple (once multiplied with m), which will then produce the smallest positive remainder (known as the preferred remainder).
This is just a complicated way of saying that there is a particular quotient value that, when multiplied by the modulus, will produce a remainder with the chosen value that will allow for the modular representation (the Rule 11 equation with the modulus operator) to be in its most simplified form. The specificities of how this "preferred muliple" (formed by the quotient and the modulus) functions are elaborated upon below.
The preferred multiple of the modulus for finding the remainder is the greatest multiple lower than the chosen number, allowing for the remainder to be as small as possible: 0 ≤ r < m. Thus, the preferred multiple is mathematically the greatest (q × m) lower than a, which means finding the correct q given that m is a constant.
The difference between the preferred multiple and the chosen number is the smallest positive remainder, which is thus the preferred remainder.
For example, with a modulus of 12, 61 would be represented as 1 mod 12, since 61 has a remainder of 1 in relation to 60, the highest multiple of 12 below 61 (meaning that 60 is the preferred multiple). With respect to a clock, this means that 61 hours after 12 A.M. would be either 1 A.M. or 1 P.M., exactly which can be determined by mod 2 of the remainder (0 for A.M.; 1 for P.M.).
As stated before, any quotient/multiple of the modulus will work for the equation (if with a larger remainder) - see Rule 13, Equivalence Classes. The preferred multiple just allows for the most simplified version of a modular representation (see Rule 15), which will be the one used in practical applications of modular arithmetic. This preferred multiple is also the one that would be most easily determined by division, as described in Rule 11.
Mathematical Definition:
(a, m) ∈ ℤ
a = (q × m) + r
Thus, a - (q × m) = r
ℤ = The set of all integers.
a = The chosen number.
q = The quotient, which produces a multiple of the modulus.
r = The remainder.
m = The modulus, the highest possible number in the set.
Explanation:
To find the remainder in a modular arithmetic system (see Rule 11) when only the chosen number and the modulus (a and m) are known, there is an exact, algorithmic definition. Note that there are two unknown variables in this equation - the quotient and the remainder (q & r). As such, the quotient will have to be determined first in order to find the remainder.
Any integer will work for the quotient (as a result of equivalence classes, which will be discussed later in Rule 13), but the preferred quotient will be the one that produces the preferred multiple (once multiplied with m), which will then produce the smallest positive remainder (known as the preferred remainder).
This is just a complicated way of saying that there is a particular quotient value that, when multiplied by the modulus, will produce a remainder with the chosen value that will allow for the modular representation (the Rule 11 equation with the modulus operator) to be in its most simplified form. The specificities of how this "preferred muliple" (formed by the quotient and the modulus) functions are elaborated upon below.
The preferred multiple of the modulus for finding the remainder is the greatest multiple lower than the chosen number, allowing for the remainder to be as small as possible: 0 ≤ r < m. Thus, the preferred multiple is mathematically the greatest (q × m) lower than a, which means finding the correct q given that m is a constant.
The difference between the preferred multiple and the chosen number is the smallest positive remainder, which is thus the preferred remainder.
For example, with a modulus of 12, 61 would be represented as 1 mod 12, since 61 has a remainder of 1 in relation to 60, the highest multiple of 12 below 61 (meaning that 60 is the preferred multiple). With respect to a clock, this means that 61 hours after 12 A.M. would be either 1 A.M. or 1 P.M., exactly which can be determined by mod 2 of the remainder (0 for A.M.; 1 for P.M.).
As stated before, any quotient/multiple of the modulus will work for the equation (if with a larger remainder) - see Rule 13, Equivalence Classes. The preferred multiple just allows for the most simplified version of a modular representation (see Rule 15), which will be the one used in practical applications of modular arithmetic. This preferred multiple is also the one that would be most easily determined by division, as described in Rule 11.
#
C. Rule .
Equivalence Classes:
While 12 ≡ 3 mod 9, it is equally true that 12 ≡ 21 mod 9, and that 12 ≡ -6 mod 9. Although these remainders may not be the preferred remainder of 3 (see Rule 12), they all still return true in the Modular Arithmetic formula (see Rule 11):
12 ≡ 3 mod 9, 3 is a valid remainder since 9|(12−3)
12 ≡ 21 mod 9, 21 is a valid remainder since 9|(12−21)
12 ≡ −6 mod 9, −6 is a valid remainder since 9|(12−(−6))
The given remainder values can all be simplified down to their smallest possible positive number using the preferred multiple of the modulus, as detailed in Rule 12. Thus, all of these modular representations are inherently equal as they all have the same 'root' preferred remainder. The set of all remainder values that behave 'equivalently' for a particular modulus form what is known as an Equivalence Class, an infinite set/series of values.
For 3 mod 9, the equivalence class of r values is an infinite set, a partial series of which is as follows:
{..., -24, -15, -6, 3, 12, 21, 30, ...}
If any of these values were to be substituted in for r (3) in 3 mod 9, it would be equivalent, the same value, because of the mod operator.
Note: There are 'm' equivalence classes for each possible remainder (0 through m-1), which collectively contain all possible integers. The difference between any two neighboring values in an equivalence class will be the modulus, as shown above.
While 12 ≡ 3 mod 9, it is equally true that 12 ≡ 21 mod 9, and that 12 ≡ -6 mod 9. Although these remainders may not be the preferred remainder of 3 (see Rule 12), they all still return true in the Modular Arithmetic formula (see Rule 11):
12 ≡ 3 mod 9, 3 is a valid remainder since 9|(12−3)
12 ≡ 21 mod 9, 21 is a valid remainder since 9|(12−21)
12 ≡ −6 mod 9, −6 is a valid remainder since 9|(12−(−6))
The given remainder values can all be simplified down to their smallest possible positive number using the preferred multiple of the modulus, as detailed in Rule 12. Thus, all of these modular representations are inherently equal as they all have the same 'root' preferred remainder. The set of all remainder values that behave 'equivalently' for a particular modulus form what is known as an Equivalence Class, an infinite set/series of values.
For 3 mod 9, the equivalence class of r values is an infinite set, a partial series of which is as follows:
{..., -24, -15, -6, 3, 12, 21, 30, ...}
If any of these values were to be substituted in for r (3) in 3 mod 9, it would be equivalent, the same value, because of the mod operator.
Note: There are 'm' equivalence classes for each possible remainder (0 through m-1), which collectively contain all possible integers. The difference between any two neighboring values in an equivalence class will be the modulus, as shown above.
#
C. Rule .
Modular Reduction:
Because any value in an equivalence class acts the same with regard to the mod operator of a given modulus, then substitutions can be made in mathematical operations that use the modulus operator, simplifying them.
Take (13 × 16) - 8, with modulus 5. While the full number can be computed (200) and an answer derived from there (0 mod 5), that is lame and time-consuming. A much cooler, faster, 21st century means of solving the problem is to substitute in for each term the simplest member of their respective equivalence classes:
13 mod 5 has a remainder of 3, and so 3 is the simplest term.
16 mod 5 has a remainder of 1, and so 1 is the simplest term.
8 mod 5 has a remainder of 3, and so 3 is the simplest term.
Therefore, the same calculation can be performed with simply (3 × 1) - 3, which returns 0 mod 5, the same answer as before, but found much easier-ly.
Note that this substitution trick does not extend equally to all mathematical operations. Exponentials, for example, cannot be simplified with the modulus:
For the problem 3⁸ mod 7, the exponent '8' cannot be simplified down to 1 mod 7. Exponents simply cannot have the substitution performed, while the base can (as shown in the example below).
For all exponentials, simplification into smaller components (using the 2nd Holy Property of Exponents - see Math Rule 66) must be performed to simplify. For ex.: 3⁸ = (3²)⁴ = (9)⁴ = (2)⁴ = 16 mod 7 = 2 mod 7, which is the answer.
Operations where equivalence class substitutions are allowed:
Multiplication
Addition
Substraction
Operations where equivalence class substitutions are banned:
Exponentials (for the exponent itself, not including the base)
Division
Because any value in an equivalence class acts the same with regard to the mod operator of a given modulus, then substitutions can be made in mathematical operations that use the modulus operator, simplifying them.
Take (13 × 16) - 8, with modulus 5. While the full number can be computed (200) and an answer derived from there (0 mod 5), that is lame and time-consuming. A much cooler, faster, 21st century means of solving the problem is to substitute in for each term the simplest member of their respective equivalence classes:
13 mod 5 has a remainder of 3, and so 3 is the simplest term.
16 mod 5 has a remainder of 1, and so 1 is the simplest term.
8 mod 5 has a remainder of 3, and so 3 is the simplest term.
Therefore, the same calculation can be performed with simply (3 × 1) - 3, which returns 0 mod 5, the same answer as before, but found much easier-ly.
Note that this substitution trick does not extend equally to all mathematical operations. Exponentials, for example, cannot be simplified with the modulus:
For the problem 3⁸ mod 7, the exponent '8' cannot be simplified down to 1 mod 7. Exponents simply cannot have the substitution performed, while the base can (as shown in the example below).
For all exponentials, simplification into smaller components (using the 2nd Holy Property of Exponents - see Math Rule 66) must be performed to simplify. For ex.: 3⁸ = (3²)⁴ = (9)⁴ = (2)⁴ = 16 mod 7 = 2 mod 7, which is the answer.
Operations where equivalence class substitutions are allowed:
Multiplication
Addition
Substraction
Operations where equivalence class substitutions are banned:
Exponentials (for the exponent itself, not including the base)
Division
#
C. Rule .
When getting a result in modular arithmetic, always simplify down to the smallest positive member of the equivalence class (see Rule 13) for your final answer. Whether for a homework/test answer or for 'in-the-field' cryptography work, it is convention to use the most simplified version of the class.
II.III Integer Rings.
#
C. Rule .
Algebraic Modular Arithmetic:
Modular Arithmetic can be defined in the form of an integer ring:
The integer ring ℤm consists of the following characteristics:
1. The set ℤm = {0, 1, ..., m-1}
2. Two arithmetic operators, "+" and "×", hold for all (a, b, c, d) ∈ ℤm such that:
i) a + b ≡ c mod m
ii) a × b ≡ d mod m
There are many overshadowing rules that every ring has to fulfill, seen in the section "RULES OF THE RING" below.
Modular Arithmetic can be defined in the form of an integer ring:
The integer ring ℤm consists of the following characteristics:
1. The set ℤm = {0, 1, ..., m-1}
2. Two arithmetic operators, "+" and "×", hold for all (a, b, c, d) ∈ ℤm such that:
i) a + b ≡ c mod m
ii) a × b ≡ d mod m
There are many overshadowing rules that every ring has to fulfill, seen in the section "RULES OF THE RING" below.
# RULES OF THE RING:
These following rules hold true for all integer rings in general, not just those pertaining to modular arithmetic.
- The ring should be closed: if any two numbers from the set are multiplied or added together, the result must be in the ring. This is ensured by the modulus operator, which always pulls the number back into the set to a value below m.
- Addition and multiplication are associative properties: For all (a, b, c) ∈ ℤm, a + (b + c) = (a + b) + c, and a × (b × c) = (a × b) × c.
- Addition is commutative for all (a, b) ∈ ℤm: a + b = b + a.
- There is an additive neutral element, 0. For all elements a ∈ ℤm, it holds that a + 0 ≡ a mod m. It is used to define the additive inverse.
- The additive inverse always exists: for any element a in the ring, there is always a negative element '-a' such that a + (-a) ≡ 0 mod m, the neutral element.
- There is a multiplicative neutral element, 1: For all elements a ∈ ℤm, it holds that a × 1 ≡ a mod m. It is used to define the multiplicative inverse.
- The Multiplicative Inverse exists only for some elements: For a ∈ ℤ, the inverse a⁻¹ is defined such that a × a⁻¹ ≡ 1 mod m. The nature of most inverses and the reasons for their occasional nonexistence are outlined in the Inverse Rules - see Rule 17 & Rule 18.
If there exists an inverse for a, then, a rare usage of division in the modular ring becomes possible: the element a⁻¹ can be divided by, as a divisor, since b/a ≡ b × a⁻¹ mod m. - The distributive property holds for all ring operations. For all (a, b, c) ∈ ℤm, a × (b + c) = (a × b) + (a × c).
Addition:
Multiplication:
#
C. Rule .
Multiplicative Inverse Eligibility Test:
To determine if an inverse exists for a specific 'a' of a particular modulus (which, for a ring, is the highest value in the set), simply find the gcd (Greatest Common Divisor) of the two values:
If gcd(a, m) = 1, then there exists a⁻¹, and a & m are said to be "relatively prime", or "coprime".
If gcd(a, m) ≠ 1, then there does NOT exist a⁻¹.
If m is prime, then gcd(a, m) will always equal to 1, for all nonzero 'a' values, and thus every 'a' value will have an inverse in that ring. The inverse of an integer completely depends on the ring, and thus the modulus.
To determine if an inverse exists for a specific 'a' of a particular modulus (which, for a ring, is the highest value in the set), simply find the gcd (Greatest Common Divisor) of the two values:
If gcd(a, m) = 1, then there exists a⁻¹, and a & m are said to be "relatively prime", or "coprime".
If gcd(a, m) ≠ 1, then there does NOT exist a⁻¹.
If m is prime, then gcd(a, m) will always equal to 1, for all nonzero 'a' values, and thus every 'a' value will have an inverse in that ring. The inverse of an integer completely depends on the ring, and thus the modulus.
#
C. Rule .
Application of Multiplicative Inverses:
Finding the Multiplicative Inverse of 'a' has the following formula (as described in RULE OF THE RING #7):
a × a⁻¹ ≡ 1 mod m
Though the multiplicative inverse of a is literally shown as a⁻¹, it is almost never the actual reciprocal of a. The reason for this is simple: All reciprocals other than -1 and 1 are not integers, and are thus not included in the set (under part 1 of the ring definition given in Rule 16).
Take a = 5, for example. The supposed inverse '1/5' is incorrect in any context, because it is not included in the set. A different inverse must be found specific to the modulus. For example, if the modulus were 7, then (as the given values pass the multiplicative eligibility test of Rule 17) the true multiplicative inverse can be found:
5 × 5⁻¹ ≡ 1 mod 7
5 × 3 ≡ 1 mod 7
5⁻¹ = 3
As shown above, when used in regards to algebraic rings, the concept of an 'inverse' bears no relation to its common usage in representing reciprocals.
Finding the Multiplicative Inverse of 'a' has the following formula (as described in RULE OF THE RING #7):
a × a⁻¹ ≡ 1 mod m
Though the multiplicative inverse of a is literally shown as a⁻¹, it is almost never the actual reciprocal of a. The reason for this is simple: All reciprocals other than -1 and 1 are not integers, and are thus not included in the set (under part 1 of the ring definition given in Rule 16).
Take a = 5, for example. The supposed inverse '1/5' is incorrect in any context, because it is not included in the set. A different inverse must be found specific to the modulus. For example, if the modulus were 7, then (as the given values pass the multiplicative eligibility test of Rule 17) the true multiplicative inverse can be found:
5 × 5⁻¹ ≡ 1 mod 7
5 × 3 ≡ 1 mod 7
5⁻¹ = 3
As shown above, when used in regards to algebraic rings, the concept of an 'inverse' bears no relation to its common usage in representing reciprocals.
#
C. Rule .
Always, as a rule of life, write denominators as (x)⁻¹ (instead of as below a line). With the importance of the inverse operation, it is always critical to recognize all denominators as just being inverses of their values. 1/a = a⁻¹.
II.IV Shift/Caesar Cipher.
#
C. Rule .
Shift Cipher:
Mathematical Definition:
(x, y, k) ∈ ℤ26
Encryption: ek(x) ≡ (x + k) mod 26
Decryption: dk(y) ≡ (y - k) mod 26
x = Plaintext message.
y = Ciphertext.
k = The Key fed into the encryption and decryption functions. Here, it represents the number of times that the characters of the plaintext are shifted rightward, using the alphabet as the set. Variations may use an expanded set, including numbers and special characters.
ℤ26 = A ring of the first 26 integers (including 0), matching the 26 characters of the alphabet. See Subsection II.III for an explanation of rings.
ek(x) = Encryption function, a mathematical formula that converts x into y.
dk(y) = Decryption function, a mathematical formula that converts y into x.
mod 26 = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to 26. Variations may use an expanded set, including numbers or special characters, in which case the '26' would change accordingly.
Explanation:
A simplified form or special case of the Substitution Cipher (Rule 10), the Shift Cipher (or Caesar Cipher) merely shifts every plaintext letter however many so positions rightward in the alphabet, wrapping around when it reaches the end (modular arithmetic!). This is occasionally known as the "ROT" Cipher (short for "rotate"), and the most well-known example is ROT13, which shifts rightward precisely halfway through the alphabet.
As a generic example, with a key of 1, some shifts would be as follows:
a -> b
b -> c
...
z -> a
As shown, once the alphabet reaches letter (26 - k) + 1, or the position in the ring ℤ26 (26 - k) (since the set begins at 0), the shift returns to the front of the alphabet.
It should be obvious to all this is an extremely unsecure cryptosystem, with a keyspace of only 26. It is vulnerable to both letter frequency analysis (previously explained in relation to Substitution Ciphers - see Rule 10) and brute-force attacks (see Rule 8).
Mathematical Definition:
(x, y, k) ∈ ℤ26
Encryption: ek(x) ≡ (x + k) mod 26
Decryption: dk(y) ≡ (y - k) mod 26
x = Plaintext message.
y = Ciphertext.
k = The Key fed into the encryption and decryption functions. Here, it represents the number of times that the characters of the plaintext are shifted rightward, using the alphabet as the set. Variations may use an expanded set, including numbers and special characters.
ℤ26 = A ring of the first 26 integers (including 0), matching the 26 characters of the alphabet. See Subsection II.III for an explanation of rings.
ek(x) = Encryption function, a mathematical formula that converts x into y.
dk(y) = Decryption function, a mathematical formula that converts y into x.
mod 26 = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to 26. Variations may use an expanded set, including numbers or special characters, in which case the '26' would change accordingly.
Explanation:
A simplified form or special case of the Substitution Cipher (Rule 10), the Shift Cipher (or Caesar Cipher) merely shifts every plaintext letter however many so positions rightward in the alphabet, wrapping around when it reaches the end (modular arithmetic!). This is occasionally known as the "ROT" Cipher (short for "rotate"), and the most well-known example is ROT13, which shifts rightward precisely halfway through the alphabet.
As a generic example, with a key of 1, some shifts would be as follows:
a -> b
b -> c
...
z -> a
As shown, once the alphabet reaches letter (26 - k) + 1, or the position in the ring ℤ26 (26 - k) (since the set begins at 0), the shift returns to the front of the alphabet.
It should be obvious to all this is an extremely unsecure cryptosystem, with a keyspace of only 26. It is vulnerable to both letter frequency analysis (previously explained in relation to Substitution Ciphers - see Rule 10) and brute-force attacks (see Rule 8).
#
C. Rule .
Vigenère Cipher
Mathematical Definition:
(x, y, k, l) ∈ ℤ26
Encryption: ek(x) ≡ (xi + ki mod l) mod 26
Decryption: dk(y) ≡ (yi - ki mod l) mod 26
x = Plaintext message.
y = Ciphertext.
k = The Key/codeword fed into the encryption and decryption functions, which, like the plaintext, is a series of letters (represented by their numerical value, 0-25) that are referred to by their i position. The key may have less, more, or the same number of characters as the plaintext (see 'l').
i = The position in the string of the plaintext, and regardless of the length of l (as a result of the mod operator), the key.
mod l = 'l' represents the length of the codeword. The mod operator functions such that if there are less characters in the codeword than in the plaintext, then the codeword characters will wrap around so that they can continue being used to produce ciphertext indefinitely.
ℤ26 = A ring of the first 26 integers (including 0), matching the 26 characters of the alphabet. See Subsection II.III for an explanation of rings.
ek(x) = Encryption function, a mathematical formula that converts x into y.
dk(y) = Decryption function, a mathematical formula that converts y into x.
mod 26 = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to 26.
Explanation:
A mere variation of the Shift cipher, in which the shift for each letter is determined by a secret codeword 'c', which has 'l' characters. Each character in the code word c represents a number of shifts rightward according to the numerical value. For example, 'a' would represent a rightward shift of zero places, while 'z' would represent a shift of 25 places.
The encryption function works as follows: Each character in the plaintext string 'x' is applied a rightward shift according to its respective letter (identical position) in the key text. This is a cyclic shift (see definition), for if the addition of the key-character value produces a number greater than 26, then the alphabet will wrap around to the beginning. For example, the plaintext character 'z' plus the codeword character 'b' will produce the ciphertext character 'a'. An interesting side-effect of this is that if the keytext is just a string of 'a' ("aaaaaaaa"), then the ciphertext will be identical to the plaintext.
The decryption function, of course, is just the opposite of the encryption function, moving each character of the ciphertext backward by the value in the positional counterpart of the code word 'c'.
Because of the way the equation is written, the key does not necessarily need to have the same number of characters as the plaintext. The mod operator on the 'l', the number of characters in the codeword, causes any short codeword to wrap around to account for any longer plaintext strings. For example, for a plaintext of "lingonberry" and a codeword of "sup", the mod operator would cause the codeword to effectively become "supsupsupsu", accounting for each character of the plaintext. Likewise, any codeward longer than the plaintext has any characters beyond the length of the plaintext ignored.
For each value of i within l, the characters of the codeword are mathematically denoted as {c0, c1, ..., cl - 1}, and the keys are similarly represented as {k0, k1, ..., kl - 1}.
Mathematical Definition:
(x, y, k, l) ∈ ℤ26
Encryption: ek(x) ≡ (xi + ki mod l) mod 26
Decryption: dk(y) ≡ (yi - ki mod l) mod 26
x = Plaintext message.
y = Ciphertext.
k = The Key/codeword fed into the encryption and decryption functions, which, like the plaintext, is a series of letters (represented by their numerical value, 0-25) that are referred to by their i position. The key may have less, more, or the same number of characters as the plaintext (see 'l').
i = The position in the string of the plaintext, and regardless of the length of l (as a result of the mod operator), the key.
mod l = 'l' represents the length of the codeword. The mod operator functions such that if there are less characters in the codeword than in the plaintext, then the codeword characters will wrap around so that they can continue being used to produce ciphertext indefinitely.
ℤ26 = A ring of the first 26 integers (including 0), matching the 26 characters of the alphabet. See Subsection II.III for an explanation of rings.
ek(x) = Encryption function, a mathematical formula that converts x into y.
dk(y) = Decryption function, a mathematical formula that converts y into x.
mod 26 = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to 26.
Explanation:
A mere variation of the Shift cipher, in which the shift for each letter is determined by a secret codeword 'c', which has 'l' characters. Each character in the code word c represents a number of shifts rightward according to the numerical value. For example, 'a' would represent a rightward shift of zero places, while 'z' would represent a shift of 25 places.
The encryption function works as follows: Each character in the plaintext string 'x' is applied a rightward shift according to its respective letter (identical position) in the key text. This is a cyclic shift (see definition), for if the addition of the key-character value produces a number greater than 26, then the alphabet will wrap around to the beginning. For example, the plaintext character 'z' plus the codeword character 'b' will produce the ciphertext character 'a'. An interesting side-effect of this is that if the keytext is just a string of 'a' ("aaaaaaaa"), then the ciphertext will be identical to the plaintext.
The decryption function, of course, is just the opposite of the encryption function, moving each character of the ciphertext backward by the value in the positional counterpart of the code word 'c'.
Because of the way the equation is written, the key does not necessarily need to have the same number of characters as the plaintext. The mod operator on the 'l', the number of characters in the codeword, causes any short codeword to wrap around to account for any longer plaintext strings. For example, for a plaintext of "lingonberry" and a codeword of "sup", the mod operator would cause the codeword to effectively become "supsupsupsu", accounting for each character of the plaintext. Likewise, any codeward longer than the plaintext has any characters beyond the length of the plaintext ignored.
For each value of i within l, the characters of the codeword are mathematically denoted as {c0, c1, ..., cl - 1}, and the keys are similarly represented as {k0, k1, ..., kl - 1}.
II.V Affine Cipher.
#
C. Rule .
Affine Cipher:
Mathematical Definition:
(x, y, a, b) ∈ ℤ26
K = (a, b)
Encryption: ek(x) ≡ ((a × x) + b) mod 26
Decryption: dk(y) ≡ (a⁻¹ × (y - b)) mod 26
x = Plaintext message.
y = Ciphertext.
K = The key, which has been split into two parts: a and b.
a = The multiplied value of the key. The number of possible 'a' values is limited by the necessity of the inverse (for the decryption function), as explained below.
a⁻¹ = The inverse of a, necessary for the decryption function.
b = The "shift parameter" value of the key, used only in addition and subtraction operations. There are 26 possible values for b, explained below.
ℤ26 = A ring of the first 26 integers (including 0), matching the 26 characters of the alphabet. See Subsection II.III for an explanation of rings.
ek(x) = Encryption function, a mathematical formula that converts x into y.
dk(y) = Decryption function, a mathematical formula that converts y into x.
mod 26 = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to 26.
Explanation:
The Affine Cipher is an attempted improvement of the shift cipher, done by complicating the encryption function through the addition of multiple parameters. However, it is still extremely easy to break. The affine cipher is performed by splitting the key into two parts:
K = (a, b)
The number of possible b values in the system is 26, as it is merely the shift parameter (as shown in the definition equations).
The number of possible a values, as a result of the inverse in the decryption function, is limited by the condition explicated in the multiplicative inverse eligibility test of Rule 17, with m being 26: only when gcd(a, 26) = 1 is 'a' an inverse, and thus contributive to the number of possible values. Counting all possible values of a (1, 3, 5, 7, 9, ...), all odd numbers 1-26 other than 13, produces an end result of 12 possible 'a' values.
The keyspace, being (#a) × (#b), is therefore 312. This remains very easy to break using a brute-force attack (see Rule 8).
Furthermore, letter frequency also remains preserved (since every instance of a particular plaintext character will be converted into the same corresponding ciphertext character, despite the minute differences in the encryption function), so a letter frequency analysis attack is also applicable.
Though multiple encryption (i.e., running the ciphertext produced by encryption function back into the encryption function to encrypt it again) will not increase the security of an affine cipher, it will for other ciphers, such as the Data Encryption Standard (see Rule 48).
Mathematical Definition:
(x, y, a, b) ∈ ℤ26
K = (a, b)
Encryption: ek(x) ≡ ((a × x) + b) mod 26
Decryption: dk(y) ≡ (a⁻¹ × (y - b)) mod 26
x = Plaintext message.
y = Ciphertext.
K = The key, which has been split into two parts: a and b.
a = The multiplied value of the key. The number of possible 'a' values is limited by the necessity of the inverse (for the decryption function), as explained below.
a⁻¹ = The inverse of a, necessary for the decryption function.
b = The "shift parameter" value of the key, used only in addition and subtraction operations. There are 26 possible values for b, explained below.
ℤ26 = A ring of the first 26 integers (including 0), matching the 26 characters of the alphabet. See Subsection II.III for an explanation of rings.
ek(x) = Encryption function, a mathematical formula that converts x into y.
dk(y) = Decryption function, a mathematical formula that converts y into x.
mod 26 = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to 26.
Explanation:
The Affine Cipher is an attempted improvement of the shift cipher, done by complicating the encryption function through the addition of multiple parameters. However, it is still extremely easy to break. The affine cipher is performed by splitting the key into two parts:
K = (a, b)
The number of possible b values in the system is 26, as it is merely the shift parameter (as shown in the definition equations).
The number of possible a values, as a result of the inverse in the decryption function, is limited by the condition explicated in the multiplicative inverse eligibility test of Rule 17, with m being 26: only when gcd(a, 26) = 1 is 'a' an inverse, and thus contributive to the number of possible values. Counting all possible values of a (1, 3, 5, 7, 9, ...), all odd numbers 1-26 other than 13, produces an end result of 12 possible 'a' values.
The keyspace, being (#a) × (#b), is therefore 312. This remains very easy to break using a brute-force attack (see Rule 8).
Furthermore, letter frequency also remains preserved (since every instance of a particular plaintext character will be converted into the same corresponding ciphertext character, despite the minute differences in the encryption function), so a letter frequency analysis attack is also applicable.
Though multiple encryption (i.e., running the ciphertext produced by encryption function back into the encryption function to encrypt it again) will not increase the security of an affine cipher, it will for other ciphers, such as the Data Encryption Standard (see Rule 48).
#
C. Rule .
Note: You can ALWAYS derive the decryption function from the encryption function of basic ciphers/algorithms. Just know that the encryption function is equal to y and the decryption function is equal to x, and you can simply isolate the appropriate variable to find whichever function you wish.
In doing so, always recall that dividing by a variable (as can occur when dividing both sides as a part of the isolation process) makes that variable into its inverse, as foretold in the lesson of Rule 19 and as demonstrated in the mathematical definition of Rule 22.
Know that when doing any algebra with an encryption/decryption equation, the mod operator will simply remain in place on whichever side it was on originally. The mod can be effectively ignored until the end of the isolation process, with it not playing a part in the moving of variables from side to side and whatnot. It will continue to act upon whichever variables are on its side of the equation.
In doing so, always recall that dividing by a variable (as can occur when dividing both sides as a part of the isolation process) makes that variable into its inverse, as foretold in the lesson of Rule 19 and as demonstrated in the mathematical definition of Rule 22.
Know that when doing any algebra with an encryption/decryption equation, the mod operator will simply remain in place on whichever side it was on originally. The mod can be effectively ignored until the end of the isolation process, with it not playing a part in the moving of variables from side to side and whatnot. It will continue to act upon whichever variables are on its side of the equation.
III. Stream Ciphers.
III.I Introduction to Stream Ciphers.
# Fig. 3. - Symmetric Cryptography Hierarchy:
A Classification hierarchy of Symmetric Cryptography. There are two major branches of Symmetric Cryptography, Block Ciphers and Stream Ciphers. See Subsection I.I for the full tree, and see Rule 7 for Cryptanalysis.
#
C. Rule .
Modular 2 Operations:
In cryptography, when considering all of the mathematical operations commonly applied in primitives and ciphers, the modular 2 operation carries with it a set of properties and a reputation that makes it unique even within modular arithmetic.
Mod 2 addition and subtraction are the same operation. Multiplication complicates things, but in all instances where the mod 2 function is limited to addition or subtraction, the results will be identical no matter which operation is applied.
With the smallest possible modulus that allows room for variation in the remainder, mod 2 operations are by and large the most popular application of modular arithmetic in cryptography. This is because their restriction of all numbers to be either 0s or 1s (by the very nature of a modular operation, see Rule 11) successfully emulates binary representation, making them extremely useful for bit-based computation (and in particular ciphers that intake streams of data, like stream ciphers (see Rule 25)).
The modular 2 operation is used so often, it has its own symbol in cryptographic diagrams: a circle with a cross. See Rule 25 for an example. In electrical engineering, the mod 2 function is known as the XOR gate, a type of binary gate (see E.E. [[[[[), further showcasing the broader importance of modular 2 operations in science as a whole.
Note that the listed properties do NOT extend to the modulus of any other number - only for two. See the Vigenère Cipher (see Rule 21), which works akin to a stream cipher, for proof using mod 26 (hint: the addition and subtraction operations produce different values).
In cryptography, when considering all of the mathematical operations commonly applied in primitives and ciphers, the modular 2 operation carries with it a set of properties and a reputation that makes it unique even within modular arithmetic.
Mod 2 addition and subtraction are the same operation. Multiplication complicates things, but in all instances where the mod 2 function is limited to addition or subtraction, the results will be identical no matter which operation is applied.
With the smallest possible modulus that allows room for variation in the remainder, mod 2 operations are by and large the most popular application of modular arithmetic in cryptography. This is because their restriction of all numbers to be either 0s or 1s (by the very nature of a modular operation, see Rule 11) successfully emulates binary representation, making them extremely useful for bit-based computation (and in particular ciphers that intake streams of data, like stream ciphers (see Rule 25)).
The modular 2 operation is used so often, it has its own symbol in cryptographic diagrams: a circle with a cross. See Rule 25 for an example. In electrical engineering, the mod 2 function is known as the XOR gate, a type of binary gate (see E.E. [[[[[), further showcasing the broader importance of modular 2 operations in science as a whole.
Note that the listed properties do NOT extend to the modulus of any other number - only for two. See the Vigenère Cipher (see Rule 21), which works akin to a stream cipher, for proof using mod 26 (hint: the addition and subtraction operations produce different values).
#
C. Rule .
Stream Ciphers
Mathematical Definition:
(xi, yi, si) ∈ ℤ2
Encryption: esi(xi) ≡ (xi + si) mod 2
Decryption: dsi(yi) ≡ (yi + si) mod 2
xi = The Plaintext bit at index i.
yi = The Ciphertext bit at index i.
si = The "Keystream" at index i, equivalent to 'k' (as in past ciphers). Here, it is the Key (at index i) fed into the encryption and decryption functions.
ℤ2 = A ring of the first 2 integers: {0, 1}. See Subsection II.III for an explanation of rings.
esi(xi) = Encryption function, a mathematical formula that converts each x bit into a y bit.
dsi(yi) = Decryption function, a mathematical formula that converts each y bit into an x bit.
mod 2 = The modulus/remainder operator with respect to 2. Numbers can only be 0 or 1 in this reality - see Rule 24 for a full treatise.
Explanation:
A cipher that encrypts bits individually, processing one bit after another in a sequence. This is opposed to a Block Cipher (see Section IV), which takes in large numbers of bits all at once.
Using the modular 2 operation (see Rule 24), the encryption and decryption functions of the basic stream cipher can be depicted as shown in Fig. 4.
The central complexity of the Stream Cipher is the generation of the "Keystream", e.g. the stream of bits with which the plaintext is encrypted. This generation must be performed through Random Numbers - see Rule 26.
If the keybit (si) is zero, then the plaintext bit will pass through unchanged, but if the keybit is 1, then the plaintext bit will flip (like binary). Thus, if the keystream (by divine intervention) is straight 0's, then the plaintext will go unencrypted.
Mathematical Definition:
(xi, yi, si) ∈ ℤ2
Encryption: esi(xi) ≡ (xi + si) mod 2
Decryption: dsi(yi) ≡ (yi + si) mod 2
xi = The Plaintext bit at index i.
yi = The Ciphertext bit at index i.
si = The "Keystream" at index i, equivalent to 'k' (as in past ciphers). Here, it is the Key (at index i) fed into the encryption and decryption functions.
ℤ2 = A ring of the first 2 integers: {0, 1}. See Subsection II.III for an explanation of rings.
esi(xi) = Encryption function, a mathematical formula that converts each x bit into a y bit.
dsi(yi) = Decryption function, a mathematical formula that converts each y bit into an x bit.
mod 2 = The modulus/remainder operator with respect to 2. Numbers can only be 0 or 1 in this reality - see Rule 24 for a full treatise.
Explanation:
A cipher that encrypts bits individually, processing one bit after another in a sequence. This is opposed to a Block Cipher (see Section IV), which takes in large numbers of bits all at once.
Using the modular 2 operation (see Rule 24), the encryption and decryption functions of the basic stream cipher can be depicted as shown in Fig. 4.
The central complexity of the Stream Cipher is the generation of the "Keystream", e.g. the stream of bits with which the plaintext is encrypted. This generation must be performed through Random Numbers - see Rule 26.
If the keybit (si) is zero, then the plaintext bit will pass through unchanged, but if the keybit is 1, then the plaintext bit will flip (like binary). Thus, if the keystream (by divine intervention) is straight 0's, then the plaintext will go unencrypted.
# Fig. 4. - Practical Stream Ciphers:
A diagram of how all practical stream ciphers (abiding by the encryption and decryption functions defined in Rule 25) function, with the modular 2 addition highlighted and the keystream generator (which varies from cipher to cipher) displayed. Note that the key distribution is not depicted.
# Keystream: A stream of characters that is combined with the plaintext to produce the ciphertext in a Stream Cipher, or, in the case of asynchronous stream ciphers, combined with a previous ciphertext to produce a new ciphertext.
The keystream is derived from the key and the seed. Generally, the keystream is denoted as "si", while the seed itself is s0, the initial position/keybit of the stream from which all recursive stream ciphers evolve from in their encryption functions. Inherently, the number of possible seeds is the same as the keyspace, since the number of seeds dictates how many keys there can be.
The creation of a keystream (both key and seed) involves random number generators, which are detailed in Subsection III.II. The seed, for example, may be created using an actual True Random Number Generator (see Rule 26), while the rest of the key will be deterministically generated from that seed using a PRNG (also Rule 26).
# Synchronous Stream Cipher: A Stream Cipher in which the keystream depends solely on the key, generated independently of the plaintext or ciphertext. Examples include Salsa20 & ChaCha.
# Asynchronous Stream Cipher: A Stream Cipher in which the keystream depends on the ciphertext in addition to the key - the key generation is reliant on previous ciphertext, making it a risky operation. An example is the Cipher Feedback (CFB) mode, described in Rule [[[.
III.II Random Number Generation.
#
C. Rule .
Random Number Generators (RNG):
The means with which a system can generate random numbers, for the purposes of constructing/filling a keystream with random bits, are split into three main mechanisms:
The means with which a system can generate random numbers, for the purposes of constructing/filling a keystream with random bits, are split into three main mechanisms:
- True Random Number Generators (TRNGs): "True" random numbers stem from random physical processes that cannot be reproduced. Such natural sources of entropy include flipping a coin, rolling a die, thermal noise, mouse movement, and keystroke timing.
Hardware and cryptographic systems have tried a lot of different techniques over the years to create a TRNG by analyzing/recording internal characteristics of the computer. Most modern CPU's have a TRNG within a TPM (trusted platform module) on the motherboard.
An example of a cipher that completely uses TRNGs (not just for one element like the seed, but for the entire keystream) is the One Time Pad, detailed in Rule 27. - Pseudo Random Number Generators (PRNGs): An RNG system that is random, but reproducable. Because PRNG's are computed, they are inherently deterministic processes. Since they are deterministic, Alice and Bob can generate the same keystream independently of one another, only needing to know the initial "seed", which is like the key for the key (see the "Keystream" definition).
With respect to Stream Ciphers, another commonly-used term is "PRBS" (Pseudo-Random Bit/Binary Sequences), which is just a more stream-specific way of looking at what these generators are actually producing.
Often, PRNG's are computed with the following function:
si+1 = f(si)
s0 = The initial seed value, which may be an actual TRNG.
f(si) = The 'randomizer' function, which performs whatever upon the seed in order to computationally randomize it.
This recursive generation is the form taken by the Linear Congruential Generator, an example of a cryptosystem utilizing a PRNG (see Rule 28).
The rand() function in C is a PRNG and uses a seed of 12345, with the following function as the randomizer:
Si+1 = ((1103515245 × si) + 12345) mod 2³¹. - Cryptographically Secure Pseudorandom Number Generators (CSPRNGs/CPRNGs): PRNG's that have an additional property: the numbers must be unpredictable.
Given n output keybits (si, si+1, ..., si+(n-1)), it is computationally infeasible to construct si+n.
While in most applications (read: the world outside cryptography), PRNG systems are perfectly fine and suited to create 'random' numbers for whatever purpose, they form very unsecure cryptosystems due to their inherently deterministic nature, and thus in Cryptography, the additional property of unpredictability is required. An example of a commonly-used CPRNG in the real world is the [[[.
# Unconditional Security: A cipher is "unconditionally secure" (or "information-theoretically secure") if it cannot be broken even with infinite computing resources.
Even if a key is 2^1000 bits, it would not be considered "unconditionally secure", because 2^1000 computers (a patently not infinite amount of computers) would be able to break the key in one second. This is despite the fact that such levels of computing power will never be realized in human history.
Thus, though there are very many ciphers that are "practically" secure (forming the backbone of our modern cybersecurity systems), they are not unconditionally secure.
# Computational Security: A cryptosystem is computationally secure if the best known algorithm for breaking it requires at least t operations, where 't' is some ridiculous number far beyond the reach of modern brute-force computational abilities.
#
C. Rule .
One Time Pad (OTP)
The One Time Pad (also referred to as the "Vernam cipher") is an example of a TRNG-based cryptosystem. It is the unconditionally secure, totally unbreakable, perfect encryption algorithm. The OTP is a stream cipher with the following properties:
1) The Keystream bits si must originate from a True Random Number Generator (a 'TRNG', see Rule 26, 1.).
2) Each Keystream bit must be used only once.
Knowledge of the Keystream must be exclusively limited to the involved parties, of course. At the end of the data transfer, the party that received the data must destroy the key so that it cannot be used by another party to decrypt the message after the fact. This is the same reason why reusing keys is extremely risky and nullifies the security benefits of the OTP.
The security of cryptosystem draws from the fact that, without knowledge of the keystream, even a brute-force attack would be futile, because any two text strings are equally as probable to be a particular word in the plaintext: if a four letter word were to be encrypted, it is equally probable for it to be "when", "stop", or "abcd".
There is one fundamental drawback of the OTP, however, that prevents its universal application: since keystream bits cannot be reused, the key has to be as long as the plaintext. A 400MB file, 8 bits to the byte, would entail a 3.2GB key. As such, the One Time Pad is not the be-all-end-all of Cryptography (at least in terms of application), and other types of CPRNGS are still relevant.
The One Time Pad (also referred to as the "Vernam cipher") is an example of a TRNG-based cryptosystem. It is the unconditionally secure, totally unbreakable, perfect encryption algorithm. The OTP is a stream cipher with the following properties:
1) The Keystream bits si must originate from a True Random Number Generator (a 'TRNG', see Rule 26, 1.).
2) Each Keystream bit must be used only once.
Knowledge of the Keystream must be exclusively limited to the involved parties, of course. At the end of the data transfer, the party that received the data must destroy the key so that it cannot be used by another party to decrypt the message after the fact. This is the same reason why reusing keys is extremely risky and nullifies the security benefits of the OTP.
The security of cryptosystem draws from the fact that, without knowledge of the keystream, even a brute-force attack would be futile, because any two text strings are equally as probable to be a particular word in the plaintext: if a four letter word were to be encrypted, it is equally probable for it to be "when", "stop", or "abcd".
There is one fundamental drawback of the OTP, however, that prevents its universal application: since keystream bits cannot be reused, the key has to be as long as the plaintext. A 400MB file, 8 bits to the byte, would entail a 3.2GB key. As such, the One Time Pad is not the be-all-end-all of Cryptography (at least in terms of application), and other types of CPRNGS are still relevant.
#
C. Rule .
Linear Congruential Generator (LCG):
Mathematical Definition:
(A, B, i, Si) ∈ ℤm
i > 0
Key K = (A, B)
Si + 1 ≡ ((A × Si) + B) mod m
S0 = The initial seed value, which may have been created using a TRNG. Of course, it is not depicted in the equation as the equation only refers to i > 0. The seed value is exactly ⌈log2 m⌉ bits long, explained below.
Si = The Keystream at index i, where i > 0. It is exactly ⌈log2 m⌉ bits long, explained below.
Si + 1 = The following value in the keystream, which is recursively calculated using the value of the previous bit in the keystream (along with the key). It is exactly ⌈log2 m⌉ bits long, explained below.
A = The multiplied value of the key. It is exactly ⌈log2 m⌉ bits long, explained below.
B = The "shift parameter" value of the key, only used for the addition operation. It is exactly ⌈log2 m⌉ bits long, explained below.
ℤm = A ring of m integers. See Subsection II.III for an explanation of rings.
mod m = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to m.
Explanation:
The LCG is a PRNG-based keystream generator, using the attributes of the key and the seed as its base components. It is an example of a non-cryptographically secure PRNG, the 2nd type of RNG detailed in Rule 26. This makes it more practical a system than the One Time Pad (see Rule 27), but much easier to break (see Rule 29). The keystream is deterministically created using a recursive function originating at S0 (the seed), which itself may be created using a TRNG.
Of course, separate from the nature of the function/equation itself, note that there are no "Encryption" or "Decryption" functions, because the given equation is merely for composing the keystream (PRNG-style - see Rule 26), while the equation for the Stream Cipher itself remains the same (see Rule 25).
The Linear Congruential Generator bears many similarities to the Affine Cipher (Rule 22), in particular how the key is split into multiple parameters (in the case of the LCG, the key used to generate the keystream). However, the length of the parameters greatly differs between the two - while affine ciphers have a set, immutable value for their keyspace, LCG variables derive their length from the modulus itself.
Note that because the modulus represents a set/ring, ℤm, m qualifies for the set-based bit-length (as detailed in Rule 4). As such, the fact that variables A, B, and Si are all ⌈log2 m⌉ bits long means that they are as long as the bit-length of the modulus.
Of course, since m is not the keyspace, ⌈log2 m⌉ is only in reference to a set-based bit-length and not to the key-length. As such, no determination regarding the keyspace of the LCG can be made from ⌈log2 m⌉, as the equation for finding it using a set-based bit-length (as extensively discussed in Rule 6) specifically requires the key-length. As a bit-based cryptosystem, the LCG does have a key-length (considering it literally generates keys), just not one equal to the bit-length of m.
⌈log2 m⌉, as the set-based bit-length of m, merely represents the total number of bits required to represent a variable who can have any value between 0 and m-1. To say that A, B, and Si all have a length of ⌈log2 m⌉ bits does not mean that they are all the same value, but just that they all use the same number of bits to represent their values. For example, 00001 and 11111 represent different values in binary, but both have a bit-length of 5.
The exact reasonings behind why each variable has a bit-length of m, and how things like the key-length and keyspace are calculated, are subject to the design choices of the Linear Congruential Generator itself. As LCGs are PRNGs, understanding the intricacies of these design choices and the exact purpose behind each part of this particular system is irrelevant to learning Cryptography.
The decisions made in designing this RNG were not made from a cryptographic standpoint, and thus warrant no in-depth analysis as to aspects like key-length and keyspace size, as the LCG will never be used in a cryptographic context.
The mathematics behind the logic for the aforementioned calculations are thoroughly complex and higher-level, and to describe them in great detail would serve no purpose in a cryptography-focused course. Rather, LCGs are useful for their discussion of how PRNGs can be cracked relatively easily (see Rule 29).
Mathematical Definition:
(A, B, i, Si) ∈ ℤm
i > 0
Key K = (A, B)
Si + 1 ≡ ((A × Si) + B) mod m
S0 = The initial seed value, which may have been created using a TRNG. Of course, it is not depicted in the equation as the equation only refers to i > 0. The seed value is exactly ⌈log2 m⌉ bits long, explained below.
Si = The Keystream at index i, where i > 0. It is exactly ⌈log2 m⌉ bits long, explained below.
Si + 1 = The following value in the keystream, which is recursively calculated using the value of the previous bit in the keystream (along with the key). It is exactly ⌈log2 m⌉ bits long, explained below.
A = The multiplied value of the key. It is exactly ⌈log2 m⌉ bits long, explained below.
B = The "shift parameter" value of the key, only used for the addition operation. It is exactly ⌈log2 m⌉ bits long, explained below.
ℤm = A ring of m integers. See Subsection II.III for an explanation of rings.
mod m = The modulus/remainder operator, which represents the usage of modular arithmetic, with all numbers represented by their remainder with respect to m.
Explanation:
The LCG is a PRNG-based keystream generator, using the attributes of the key and the seed as its base components. It is an example of a non-cryptographically secure PRNG, the 2nd type of RNG detailed in Rule 26. This makes it more practical a system than the One Time Pad (see Rule 27), but much easier to break (see Rule 29). The keystream is deterministically created using a recursive function originating at S0 (the seed), which itself may be created using a TRNG.
Of course, separate from the nature of the function/equation itself, note that there are no "Encryption" or "Decryption" functions, because the given equation is merely for composing the keystream (PRNG-style - see Rule 26), while the equation for the Stream Cipher itself remains the same (see Rule 25).
The Linear Congruential Generator bears many similarities to the Affine Cipher (Rule 22), in particular how the key is split into multiple parameters (in the case of the LCG, the key used to generate the keystream). However, the length of the parameters greatly differs between the two - while affine ciphers have a set, immutable value for their keyspace, LCG variables derive their length from the modulus itself.
Note that because the modulus represents a set/ring, ℤm, m qualifies for the set-based bit-length (as detailed in Rule 4). As such, the fact that variables A, B, and Si are all ⌈log2 m⌉ bits long means that they are as long as the bit-length of the modulus.
Of course, since m is not the keyspace, ⌈log2 m⌉ is only in reference to a set-based bit-length and not to the key-length. As such, no determination regarding the keyspace of the LCG can be made from ⌈log2 m⌉, as the equation for finding it using a set-based bit-length (as extensively discussed in Rule 6) specifically requires the key-length. As a bit-based cryptosystem, the LCG does have a key-length (considering it literally generates keys), just not one equal to the bit-length of m.
⌈log2 m⌉, as the set-based bit-length of m, merely represents the total number of bits required to represent a variable who can have any value between 0 and m-1. To say that A, B, and Si all have a length of ⌈log2 m⌉ bits does not mean that they are all the same value, but just that they all use the same number of bits to represent their values. For example, 00001 and 11111 represent different values in binary, but both have a bit-length of 5.
The exact reasonings behind why each variable has a bit-length of m, and how things like the key-length and keyspace are calculated, are subject to the design choices of the Linear Congruential Generator itself. As LCGs are PRNGs, understanding the intricacies of these design choices and the exact purpose behind each part of this particular system is irrelevant to learning Cryptography.
The decisions made in designing this RNG were not made from a cryptographic standpoint, and thus warrant no in-depth analysis as to aspects like key-length and keyspace size, as the LCG will never be used in a cryptographic context.
The mathematics behind the logic for the aforementioned calculations are thoroughly complex and higher-level, and to describe them in great detail would serve no purpose in a cryptography-focused course. Rather, LCGs are useful for their discussion of how PRNGs can be cracked relatively easily (see Rule 29).
#
C. Rule .
HOW TO CRACK A LINEAR CONGRUENTIAL GENERATOR (LCG):
In order to crack a rudimentary LCG system and discover the full keystream to decrypt the system, the attacker only needs to know three characters of the plaintext that were encrypted (along with all of the ciphertext). Generally, in encrypting a document (such as Microsoft Word or Excel), there will be file or protocol header information at the start (like the version number), which will always be the same initial symbols being encrypted. Therefore, knowledge of the attacker of these plaintext characters, in addition to the ciphertext, can be assumed.
With knowledge of the LCG key-stream equation, the attacker would know S0, S1, and S2 only. There would thus be three unknowns: A, B, and m. However, the set of commonly used m values is relatively small (see list), and so iterating through them using brute-force (once A and B have been discovered) would be very simple: simply calculate the associated keystream for each possible m value, then check each keystream using the stream cipher decryption function (see Rule 25) and the known ciphertext, until the correct keystream (and thus m value) is found. Thus, m is considered one of the known variables.
The attacker only has to create a system of equations-style problem (using the three known plaintext characters and the ciphertext) in order to isolate A and B, respectively.
S1 ≡ ((A × S0) + B) mod m
S2 ≡ ((A × S1) + B) mod m
A = ((S1 - S2) × (S0 - S1)⁻¹) mod m
B = (S1 - (S0 × (S1 - S2) × (S0 - S1)⁻¹)) mod m
After finding A and B, all that would be left to be done is to brute-force m as previously described, and the system would be cracked. The full plaintext would be able to be decoded since every variable of the LCG would be known.
In order to crack a rudimentary LCG system and discover the full keystream to decrypt the system, the attacker only needs to know three characters of the plaintext that were encrypted (along with all of the ciphertext). Generally, in encrypting a document (such as Microsoft Word or Excel), there will be file or protocol header information at the start (like the version number), which will always be the same initial symbols being encrypted. Therefore, knowledge of the attacker of these plaintext characters, in addition to the ciphertext, can be assumed.
With knowledge of the LCG key-stream equation, the attacker would know S0, S1, and S2 only. There would thus be three unknowns: A, B, and m. However, the set of commonly used m values is relatively small (see list), and so iterating through them using brute-force (once A and B have been discovered) would be very simple: simply calculate the associated keystream for each possible m value, then check each keystream using the stream cipher decryption function (see Rule 25) and the known ciphertext, until the correct keystream (and thus m value) is found. Thus, m is considered one of the known variables.
The attacker only has to create a system of equations-style problem (using the three known plaintext characters and the ciphertext) in order to isolate A and B, respectively.
S1 ≡ ((A × S0) + B) mod m
S2 ≡ ((A × S1) + B) mod m
A = ((S1 - S2) × (S0 - S1)⁻¹) mod m
B = (S1 - (S0 × (S1 - S2) × (S0 - S1)⁻¹)) mod m
After finding A and B, all that would be left to be done is to brute-force m as previously described, and the system would be cracked. The full plaintext would be able to be decoded since every variable of the LCG would be known.
III.III Fundamentals of Linear Feedback Shift Registers.
Linear Feedback Shift Registers (LFSRs) are a type of keystream generator, and are fundamentally important primitives that serve as the building blocks of many ciphers. There is a large amount of terminology used with LFSRs that obfuscates the readability and coherency of any text describing them. Worse, some phrases/terms are more selectively applied than others and/or share meanings.
As such, to better adumbrate LFSRs to the beginning Cryptographer, all known LFSR-specific terminologies are described in detail within Subsections III.III & III.IV (alongside all prerequisite E.E. knowledge for LFSRs), legible for both straight-through reading (as you would approach a standard textbook) and for the 'ctrl-f'ing Cryptographer who encountered an unfamiliar term in the field.
# Clocked Storage Element (CSE): A storage container that captures information at a specific moment in time, storing it until needed. Think of it like a recording device built into the hardware of the computer, and it captures information at the moment a signal is sent to it (updating to replace whatever information was in it previously).
In more explicitly electrical engineering terms (for those more experienced in such regards), CSE's are part of Clocking Subsystems (see E.E. Rule [[[[[) and respond to Clock signals (see E.E. Rule [[[[[).
#
C. Rule .
A "Flip-flop" is a clocked storage element that stores a single bit. There is an input, an output, and a Clock Input that determines whether any inputted bit is to be stored or not.
The general symbology used in diagrams for a flip-flop (in which D is the input & Q is the output) is as follows:
A diagram of the basic functions of the flip-flop electrical component. D is the input, Q is the output. Ignore the Q with the line for now ([[[). Courtesy of buildcircuitelectronics.
And here is a diagram showing how the output relies on clock signals to accept an input change, if any:
A diagram detailing how the clock signal will influence what data from the input is stored and produced in the output. As shown, the flip-flop will only store the first event captured in the input when the clock signal becomes active, regardless of whether the input changes while the clock signal is still active. Courtesy of Wikipedia.
The general symbology used in diagrams for a flip-flop (in which D is the input & Q is the output) is as follows:
A diagram of the basic functions of the flip-flop electrical component. D is the input, Q is the output. Ignore the Q with the line for now ([[[). Courtesy of buildcircuitelectronics.
And here is a diagram showing how the output relies on clock signals to accept an input change, if any:
A diagram detailing how the clock signal will influence what data from the input is stored and produced in the output. As shown, the flip-flop will only store the first event captured in the input when the clock signal becomes active, regardless of whether the input changes while the clock signal is still active. Courtesy of Wikipedia.
#
C. Rule .
Shift Registers:
A "shift register" is a concatentation of several individual flip-flops. Each flip-flop has a starting bit-value, which it then uses to send a signal to each following flip-flop until the final one, which will produce each bit of the output. The combined bits taken from the final flip-flop form a keystream, as depicted in the diagram below. The shift register is one half of an LFSR (see Rule 32).
Very important to notice in the progress of the bits of a shift register towards the output, is that there is a distinct pattern that holds for each bit-value (placed below the flip-flops on the diagram), known as the Diagonal Rule: each bit-value will be translated diagonally rightward and downward, for as many flip-flops as there are to the right. Note this pattern in the diagram below:
An example of a shift register, with three flip-flops, with every new value sent receiving a clock signal:
A shift register, complete with three flip-flops, and a starting value of 1-0-0. Data moves rightward as the result of a clock signal allowing each flip-flop to take in the data of the flip-flop to its left, and the Diagonal rule becomes visible in how the data values effectively move diagonally to the right from their initial position.
A "shift register" is a concatentation of several individual flip-flops. Each flip-flop has a starting bit-value, which it then uses to send a signal to each following flip-flop until the final one, which will produce each bit of the output. The combined bits taken from the final flip-flop form a keystream, as depicted in the diagram below. The shift register is one half of an LFSR (see Rule 32).
Very important to notice in the progress of the bits of a shift register towards the output, is that there is a distinct pattern that holds for each bit-value (placed below the flip-flops on the diagram), known as the Diagonal Rule: each bit-value will be translated diagonally rightward and downward, for as many flip-flops as there are to the right. Note this pattern in the diagram below:
An example of a shift register, with three flip-flops, with every new value sent receiving a clock signal:
A shift register, complete with three flip-flops, and a starting value of 1-0-0. Data moves rightward as the result of a clock signal allowing each flip-flop to take in the data of the flip-flop to its left, and the Diagonal rule becomes visible in how the data values effectively move diagonally to the right from their initial position.
III.IV Linear Feedback Shift Registers.
There is an inherent relationship between electrical engineering and Cryptography, specifically in how Cryptography developed: in the early days of the development of the Stream Cipher, the goal was to create a 'small' stream cipher, e.g. a stream cipher that could be implemented in hardware without using too much power.
Today, all stream ciphers fit one of two categories: ciphers optimized for software implementation, and ciphers optimized for hardware implementation. A prime example of the latter are "Shift Register-Based Stream Ciphers", in particular shift registers (see Rule 31) with a feedback mechanism, better known as Linear Feedback Shift Registers.
#
C. Rule .
Linear Feedback Shift Registers:
Mathematical Definition:
The equation depends on the specific characteristics of the LFSR. Specifically, the number of flip-flops, the number of mod 2 functions, and which flip-flops have mod 2 functions. The following formula applies to all LFSRs and is fully explained/derived in the LFSR Generalization (see Rule 33):
(Si, Pj) ∈ ℤ2
(i, j) ∈ ℤm
$$S_{m+i} \equiv \left( \sum_{j=0}^{m-1} S_{i+j} \times P_{j} \right) \mod 2$$
m = The number of flip-flops in the LFSR. This number determines both the length of the state register and the period (see Rule 34) of the output sequence.
i = The offset in the shift register, i.e., the number bit of the keystream that is being found. This is why it is ∈ ℤm - it can go no greater than m-1.
Sm + i = The bit inputted into the first flip-flop at the offset i, and outputted into the keystream at the offset m+i. That's the diagonal rule for you.
j = The index variable for each individual flip-flop, each of which has the potential to contribute to the feedback path, as determined by the feedback coefficient.
Si + j = The bit held by a particular flip-flop j at a specific offset i in the shift register. This is the value being inputted into the multiplier function from the flip-flop.
Pj = The feedback coefficient of the multiplier associated with flip-flop j. Either 0 or 1.
mod 2 = The modulus/remainder operator with respect to 2. Numbers can only be 0 or 1 in this reality - see Rule 24 for a full treatise.
Explanation:
Occasionally referred to as cryptographic "linear recurrences" by various demented individuals, Linear Feedback Shift Registers are yet another PRNG-based keystream generator, and are thus crackable with some effort (see Rule 39).
However, unlike other PRNGS like Linear Congruential Generators (see Rule 28) which have no function in real cryptography due to their absurd unsecurity, the LFSR finds application in many ciphers due to its usefulness as a primitive. These ciphers use multiple LFSRs to achieve greater security: the A51 cipher (see Rule [[[), for example, consists of 3. This greatly enhances the security of the cipher and validates the usage of LFSRs for legitimate cryptographic purposes (see Rule [[[).
LFSRs incorporate a standard Shift Register (as detailed in Rule 31) alongside a feedback mechanism/path, generating fresh input for the first flip-flop using some output data. The feedback path extends from the output of the rightmost flip-flop (which, as known from the shift register analysis in Rule 31, is the flip-flop whose bits form the keystream) and inputs into the first flip-flop.
Placed along the feedback path are modular 2 addition functions (a.k.a. XOR gates, detailed in Rule 24), which are performed between the bit from the final flip-flop (by virtue of it being the beginning of the feedback path) and atleast one other in the shift register. Multiple XOR-gates can be added along the feedback path to create additional mod 2 operations (inherently meaning mod 2 operations involving the product of another mod 2 operation from earlier along the feedback path), complicating the structure of the LFSR and enraging Oscar.
The mod 2 calculation is first performed in the initial state of the shift register (the "initialization vector" of the shift register - see the "State" definition), before the first clock cycle, pre-computing the value that will be used as input for the first flip-flop on the first clock cycle. Every clock cycle adds another row of bits below the flip-flops, accounting for the clock signals sent to each flip-flop and their subsequent outputs.
Once the bit travels all the way through the feedback path, having been XOR'd 1+ times with the bits from various points in the register, it is simply fed into the first flip-flop so that the shift register can have a new input value. The value of the bit inputted into the first flip-flop is the result of the summation of all of the possible XOR operations that could be present in the LFSR.
Since Shift Registers are an integral component of LFSRs, the Diagonal Rule previously described for Shift Registers (see Rule 31) is retained for the movement of bits within an LFSR, as shown in the diagram below:
A Linear Feedback Shift Register, complete with three flip-flops and a full period of values, which compose one complete keystream.
The specific mathematical formula of the keystream produced by the depicted LFSR is (as a result of the diagonal rule): Si+3 ≡ (si+1 + si) mod 2.
Mathematical Definition:
The equation depends on the specific characteristics of the LFSR. Specifically, the number of flip-flops, the number of mod 2 functions, and which flip-flops have mod 2 functions. The following formula applies to all LFSRs and is fully explained/derived in the LFSR Generalization (see Rule 33):
(Si, Pj) ∈ ℤ2
(i, j) ∈ ℤm
$$S_{m+i} \equiv \left( \sum_{j=0}^{m-1} S_{i+j} \times P_{j} \right) \mod 2$$
m = The number of flip-flops in the LFSR. This number determines both the length of the state register and the period (see Rule 34) of the output sequence.
i = The offset in the shift register, i.e., the number bit of the keystream that is being found. This is why it is ∈ ℤm - it can go no greater than m-1.
Sm + i = The bit inputted into the first flip-flop at the offset i, and outputted into the keystream at the offset m+i. That's the diagonal rule for you.
j = The index variable for each individual flip-flop, each of which has the potential to contribute to the feedback path, as determined by the feedback coefficient.
Si + j = The bit held by a particular flip-flop j at a specific offset i in the shift register. This is the value being inputted into the multiplier function from the flip-flop.
Pj = The feedback coefficient of the multiplier associated with flip-flop j. Either 0 or 1.
mod 2 = The modulus/remainder operator with respect to 2. Numbers can only be 0 or 1 in this reality - see Rule 24 for a full treatise.
Explanation:
Occasionally referred to as cryptographic "linear recurrences" by various demented individuals, Linear Feedback Shift Registers are yet another PRNG-based keystream generator, and are thus crackable with some effort (see Rule 39).
However, unlike other PRNGS like Linear Congruential Generators (see Rule 28) which have no function in real cryptography due to their absurd unsecurity, the LFSR finds application in many ciphers due to its usefulness as a primitive. These ciphers use multiple LFSRs to achieve greater security: the A51 cipher (see Rule [[[), for example, consists of 3. This greatly enhances the security of the cipher and validates the usage of LFSRs for legitimate cryptographic purposes (see Rule [[[).
LFSRs incorporate a standard Shift Register (as detailed in Rule 31) alongside a feedback mechanism/path, generating fresh input for the first flip-flop using some output data. The feedback path extends from the output of the rightmost flip-flop (which, as known from the shift register analysis in Rule 31, is the flip-flop whose bits form the keystream) and inputs into the first flip-flop.
Placed along the feedback path are modular 2 addition functions (a.k.a. XOR gates, detailed in Rule 24), which are performed between the bit from the final flip-flop (by virtue of it being the beginning of the feedback path) and atleast one other in the shift register. Multiple XOR-gates can be added along the feedback path to create additional mod 2 operations (inherently meaning mod 2 operations involving the product of another mod 2 operation from earlier along the feedback path), complicating the structure of the LFSR and enraging Oscar.
The mod 2 calculation is first performed in the initial state of the shift register (the "initialization vector" of the shift register - see the "State" definition), before the first clock cycle, pre-computing the value that will be used as input for the first flip-flop on the first clock cycle. Every clock cycle adds another row of bits below the flip-flops, accounting for the clock signals sent to each flip-flop and their subsequent outputs.
Once the bit travels all the way through the feedback path, having been XOR'd 1+ times with the bits from various points in the register, it is simply fed into the first flip-flop so that the shift register can have a new input value. The value of the bit inputted into the first flip-flop is the result of the summation of all of the possible XOR operations that could be present in the LFSR.
Since Shift Registers are an integral component of LFSRs, the Diagonal Rule previously described for Shift Registers (see Rule 31) is retained for the movement of bits within an LFSR, as shown in the diagram below:
A Linear Feedback Shift Register, complete with three flip-flops and a full period of values, which compose one complete keystream.
The specific mathematical formula of the keystream produced by the depicted LFSR is (as a result of the diagonal rule): Si+3 ≡ (si+1 + si) mod 2.
# Feedback Path/Feedback Mechanism: The path that allows for bits to be inputted back into the Linear Feedback Shift Register using output data, forming the "Linear Feedback" part of the LFSR. The path extends from the output of the rightmost flip-flop and inputs into the first flip-flop.
Placed along the feedback path are modular 2 addition functions (a.k.a. XOR gates, detailed in Rule 24), which are performed between the bit from the final flip-flop (by virtue of it being the beginning of the feedback path) and atleast one other in the shift register.
# State/Offset (in regard to LFSRs): The bits of the flip-flops at a particular row-position in the shift register. Given knowledge of an LFSR state and the XOR-positions/feedback path, every following row of bits can be determined.
The first state of an LFSR is known as the Initialization Vector.
Even without knowledge of the XOR positions, by pure knowledge of the first state, almost every flip-flop bit in the following state (except for the first F.F., the recipient of the input of the feedback state) can be determined, as a result of the diagonal rule of Shift Registers (see Rule 31).
# Taps/Tap Sequences: Know that there are alternate terminologies used in more pretentious and snobbish cryptographic circles. In these contexts, each outputted bit is referred to as a tap, while the full list of taps is known as the tap sequence. In the Summary of Cryptography, for the sake of simplicity, these terms will only be referred to as the "output bits" and "keystream", respectively.
#
C. Rule .
LFSR Generalization:
To construct a generalized LFSR so that a general equation can be applied, several new mathematical operations must be introduced.
First, the number of flip-flops in the register can be generalized to an arbitrary 'm' value.
The second generalization is a bit more complex: Understand that it is possible for any flip-flop in an LFSR to have its bits fed into an XOR gate on the feedback path, and for there to be as many XOR gates as flip-flops (minus one, since the rightmost flip-flops share one). Since every flip-flop can have an XOR gate (and thus be apart of the feedback path), a multiplier function (labeled P0 to Pm-1) is added along each flip-flop's tentative connection to the feedback path, serving as an intermediary between the flip-flop and any possible XOR gate above on the feedback path. The multiplier essentially acts as an on-or-off switch, activating depending on whether there actually is an XOR gate for that particular flip-flop or not, as detailed below.
A generalized LFSR, with every possible link between a flip-flop and the feedback path having a multiplier function, serving as the 'switch' determining whether that flip-flop is included as a part of the XOR operation.
The multiplier function works by multiplying the value of the flip-flop by an internal P-value, known as the "feedback coefficient". The feedback coefficient, referred to as pi, is a value within the multiplier that only has two possible values: 1 if there is a XOR gate, and 0 if there isn't. Mathematically, this means that the feedback coefficient can only be a binary value: pi ∈ ℤ2.
The feedback coefficient is determined by whether the flip-flop actually has an XOR gate connected to it or not. For example, in the given diagram, every flip-flop has a corresponding XOR gate connected to it just above the multiplier, while in the diagram of Rule 32, only the middle flip-flop has an XOR gate.
Mathematically, the principal effect of the feedback coefficient lies in how it decides what value is outputted by the multiplier towards the feedback path. Specifically, the feedback coefficient (pi) is the determining factor in the multiplier equation: O = pi × I.
'I' refers to the bit inputted into the multiplier by the flip-flop (i.e., its bit-value at that particular clock cycle), and 'O' represents the output of the multiplier into the feedback path. As evident (and as detailed below), whether pi is 0 or 1 is the determining factor in whether the input is the same as the output.
If there IS an XOR gate for that flip-flop, and thus a connection to the feedback path, then the feedback coefficient will equal 1, since the input is equal to the output: O = pi × I = I.
If there's NO XOR gate, then the feedback coefficient will equal 0, since the output O must be equal to 0 in order for the inputted bit to have no impact on the feedback path. The output O is equal to 0, and since O = pi × I, and as I is not necessarily 0, then pi must equal 0.
In this way, the multiplier is like a border checkpoint, and the feedback coefficient is the inspector. If the XOR gate exists for the flip-flop that multiplier is serving, then the bit is granted unimpeded passage into the gate by the feedback coefficient. However, if no XOR gate exists, then the bit is effectively turned away; by altering the bit to 0, it is made irrelevant to the feedback path, since an addition of zero (the additive neutral element as detailed in the "Rules of the Ring" of Subsection II.III) contributes nothing to the end-result bit of the feedback path (that which is inputted into the leftmost flip-flop).
For the following formula, you must know two things about Sm: It is the sum of all of the XOR operations performed before the first clock cycle, i.e. the preloaded bit-value that is ready to be inputted into the first flip-flop after the initialization vector, and it doubles as the first outbit bit into the keystream that can be computed using the LFSR equation. Every S value before Sm is part of the initalization vector (as a result of the diagonal rule), which, of course, is composed of non-deterministic seed values which cannot be calculated.
Thus, after the first clock cycle, the second sum of every XOR operation performed along the feedback path (which, of course, involves a different set of bits (as a result of the second state) and produces the second bit-value inputted into the first flip-flop) will be Sm+1, and so on. This formula synthesizes every generalization made throughout the course of this Rule into a cohesive and elegant little package:
Mathematical Definition:
(Si, Pj) ∈ ℤ2
(i, j) ∈ ℤm
$$S_{m+i} \equiv \left( \sum_{j=0}^{m-1} S_{i+j} \times P_{j} \right) \mod 2$$
m = The number of flip-flops in the LFSR. This number determines both the length of the state register and the period (see Rule 34) of the output sequence.
i = The offset in the shift register, i.e., the number bit of the keystream that is being found. This is why it is ∈ ℤm - it can go no greater than m-1.
Sm + i = The bit inputted into the first flip-flop at the offset i, and outputted into the keystream at the offset m+i. That's the diagonal rule for you.
j = The index variable for each individual flip-flop, each of which has the potential to contribute to the feedback path, as determined by the feedback coefficient.
Si + j = The bit held by a particular flip-flop j at a specific offset i in the shift register. This is the value being inputted into the multiplier function from the flip-flop.
Pj = The feedback coefficient of the multiplier associated with flip-flop j. Either 0 or 1.
mod 2 = The modulus/remainder operator with respect to 2. Numbers can only be 0 or 1 in this reality - see Rule 24 for a full treatise.
To construct a generalized LFSR so that a general equation can be applied, several new mathematical operations must be introduced.
First, the number of flip-flops in the register can be generalized to an arbitrary 'm' value.
The second generalization is a bit more complex: Understand that it is possible for any flip-flop in an LFSR to have its bits fed into an XOR gate on the feedback path, and for there to be as many XOR gates as flip-flops (minus one, since the rightmost flip-flops share one). Since every flip-flop can have an XOR gate (and thus be apart of the feedback path), a multiplier function (labeled P0 to Pm-1) is added along each flip-flop's tentative connection to the feedback path, serving as an intermediary between the flip-flop and any possible XOR gate above on the feedback path. The multiplier essentially acts as an on-or-off switch, activating depending on whether there actually is an XOR gate for that particular flip-flop or not, as detailed below.
A generalized LFSR, with every possible link between a flip-flop and the feedback path having a multiplier function, serving as the 'switch' determining whether that flip-flop is included as a part of the XOR operation.
The multiplier function works by multiplying the value of the flip-flop by an internal P-value, known as the "feedback coefficient". The feedback coefficient, referred to as pi, is a value within the multiplier that only has two possible values: 1 if there is a XOR gate, and 0 if there isn't. Mathematically, this means that the feedback coefficient can only be a binary value: pi ∈ ℤ2.
The feedback coefficient is determined by whether the flip-flop actually has an XOR gate connected to it or not. For example, in the given diagram, every flip-flop has a corresponding XOR gate connected to it just above the multiplier, while in the diagram of Rule 32, only the middle flip-flop has an XOR gate.
Mathematically, the principal effect of the feedback coefficient lies in how it decides what value is outputted by the multiplier towards the feedback path. Specifically, the feedback coefficient (pi) is the determining factor in the multiplier equation: O = pi × I.
'I' refers to the bit inputted into the multiplier by the flip-flop (i.e., its bit-value at that particular clock cycle), and 'O' represents the output of the multiplier into the feedback path. As evident (and as detailed below), whether pi is 0 or 1 is the determining factor in whether the input is the same as the output.
If there IS an XOR gate for that flip-flop, and thus a connection to the feedback path, then the feedback coefficient will equal 1, since the input is equal to the output: O = pi × I = I.
If there's NO XOR gate, then the feedback coefficient will equal 0, since the output O must be equal to 0 in order for the inputted bit to have no impact on the feedback path. The output O is equal to 0, and since O = pi × I, and as I is not necessarily 0, then pi must equal 0.
In this way, the multiplier is like a border checkpoint, and the feedback coefficient is the inspector. If the XOR gate exists for the flip-flop that multiplier is serving, then the bit is granted unimpeded passage into the gate by the feedback coefficient. However, if no XOR gate exists, then the bit is effectively turned away; by altering the bit to 0, it is made irrelevant to the feedback path, since an addition of zero (the additive neutral element as detailed in the "Rules of the Ring" of Subsection II.III) contributes nothing to the end-result bit of the feedback path (that which is inputted into the leftmost flip-flop).
For the following formula, you must know two things about Sm: It is the sum of all of the XOR operations performed before the first clock cycle, i.e. the preloaded bit-value that is ready to be inputted into the first flip-flop after the initialization vector, and it doubles as the first outbit bit into the keystream that can be computed using the LFSR equation. Every S value before Sm is part of the initalization vector (as a result of the diagonal rule), which, of course, is composed of non-deterministic seed values which cannot be calculated.
Thus, after the first clock cycle, the second sum of every XOR operation performed along the feedback path (which, of course, involves a different set of bits (as a result of the second state) and produces the second bit-value inputted into the first flip-flop) will be Sm+1, and so on. This formula synthesizes every generalization made throughout the course of this Rule into a cohesive and elegant little package:
Mathematical Definition:
(Si, Pj) ∈ ℤ2
(i, j) ∈ ℤm
$$S_{m+i} \equiv \left( \sum_{j=0}^{m-1} S_{i+j} \times P_{j} \right) \mod 2$$
m = The number of flip-flops in the LFSR. This number determines both the length of the state register and the period (see Rule 34) of the output sequence.
i = The offset in the shift register, i.e., the number bit of the keystream that is being found. This is why it is ∈ ℤm - it can go no greater than m-1.
Sm + i = The bit inputted into the first flip-flop at the offset i, and outputted into the keystream at the offset m+i. That's the diagonal rule for you.
j = The index variable for each individual flip-flop, each of which has the potential to contribute to the feedback path, as determined by the feedback coefficient.
Si + j = The bit held by a particular flip-flop j at a specific offset i in the shift register. This is the value being inputted into the multiplier function from the flip-flop.
Pj = The feedback coefficient of the multiplier associated with flip-flop j. Either 0 or 1.
mod 2 = The modulus/remainder operator with respect to 2. Numbers can only be 0 or 1 in this reality - see Rule 24 for a full treatise.
#
C. Rule .
The Period is the length of the longest string of numbers before repeating in the keystream generated by an LFSR. It is thus also the number of possible offsets a LFSR can have before repeating a single one. For example, in a particular LFSR with 3 flip-flops (specifically the one given in Rule 32), the keystream is as follows:
001011100101110010111001011100101...
As seen, the keystream is just a string of "0010111" that repeats infinitely, meaning that the LFSR has a period of 7.
A simple principle can thus be derived: The maximum possible period (or sequence length) generated by an LFSR of degree m is 2m - 1.
As soon as a previous bit pattern/sequence (a 'state') is reached, the cycle will repeat itself, forming a 'state loop'. Only certain feedback configurations (Pm-1, ..., P0) yield maximum length periods, which will be maximum regardless of the initialization vector (!). For any non-maximum-period LFSR however, the initalization vector will affect how long the period is, as different initial states will result in state loops of different lengths.
For an example, consider a LFSR with five flip-flops and a non-maximum feedback configuration. With one initialization vector, the LFSR could have its states repeat after only three distinct rows, and for another initialization vector, could have its states repeat after ten distinct rows, all the while having the same feedback configuration. Different initialization vectors produce different state loops when the LFSR does not have a maximum-length feedback configuration.
This is why the given value is the maximum possible period of an LFSR - only some reach it. Furthermore, the reason for the "- 1" in the equation is because the maximum period incorporates all possible offsets except for one: 000. As detailed in Rule 35, it is impossible for an all-zeroes row to appear in an LFSR, and thus the highest period an LFSR can strive for is 2m - 1.
There are patterns within the LFSR, specifically that of the positioning of the XOR gates with respect to the degree m, that can be used to determine if an LFSR will produce a maximum-length period or not - see Rule 38 for more information. These patterns require knowledge of the Polynomial Representation of LFSRs - see Rule 37.
001011100101110010111001011100101...
As seen, the keystream is just a string of "0010111" that repeats infinitely, meaning that the LFSR has a period of 7.
A simple principle can thus be derived: The maximum possible period (or sequence length) generated by an LFSR of degree m is 2m - 1.
As soon as a previous bit pattern/sequence (a 'state') is reached, the cycle will repeat itself, forming a 'state loop'. Only certain feedback configurations (Pm-1, ..., P0) yield maximum length periods, which will be maximum regardless of the initialization vector (!). For any non-maximum-period LFSR however, the initalization vector will affect how long the period is, as different initial states will result in state loops of different lengths.
For an example, consider a LFSR with five flip-flops and a non-maximum feedback configuration. With one initialization vector, the LFSR could have its states repeat after only three distinct rows, and for another initialization vector, could have its states repeat after ten distinct rows, all the while having the same feedback configuration. Different initialization vectors produce different state loops when the LFSR does not have a maximum-length feedback configuration.
This is why the given value is the maximum possible period of an LFSR - only some reach it. Furthermore, the reason for the "- 1" in the equation is because the maximum period incorporates all possible offsets except for one: 000. As detailed in Rule 35, it is impossible for an all-zeroes row to appear in an LFSR, and thus the highest period an LFSR can strive for is 2m - 1.
There are patterns within the LFSR, specifically that of the positioning of the XOR gates with respect to the degree m, that can be used to determine if an LFSR will produce a maximum-length period or not - see Rule 38 for more information. These patterns require knowledge of the Polynomial Representation of LFSRs - see Rule 37.
#
C. Rule .
The only string of bits that can never appear in an LFSR state is straight 0's. Such a thing is only possible if the initial setting is all straight 0's, which is a ridiculous thought not to be entertained.
# Primitive Polynomials: A special type of irreducible polynomial. An irreducible polynomial is akin to a "prime" polynomial, with the only factors being 1 and the polynomial itself. While the application of primitive polynomials in Cryptography is fairly extensive (as seen in Rule 36 & Rule 38), a more detailed analysis of them (and the exact difference between them and irreducible polynomials) can be found in Math Rule [[[.
#
C. Rule .
Types of LFSRs:
In practice, there are three types of LFSRs, the properties of which are the result of the feedback coefficients and degree.
In practice, there are three types of LFSRs, the properties of which are the result of the feedback coefficients and degree.
- Primitive Polynomial-based: These LFSRs are composed of primitive polynomials (see definition), and produce a maximum-length period, the only LFSRs to do so.
- Non-Primitive Irreducible Polynomial-based: Using irreducible polynomials that are not "primitive", these LFSRs produce a period that is totally independent of the initial value/"state" of the register. These algorithms do not produce maximum-length sequences.
- Reducible Polynomial-based: These LFSRs have a sequence/period dependent on the initial state of the register. Of course, these algorithms can never produce a maximum-length sequence.
#
C. Rule .
Polynomial Representation of LFSRs:
All that is needed to represent a LFSR mathematically (aside from the initialization vector) is the degree m (the number of flip-flops), and the feedback coefficients. These characteristics can be represented in polynomial form as so:
P(x) = xm + Pm-1 × xm-1 + ... + P1 × x + P0
m = The number of flip-flops.
x = The simple polynomial variable, nothing to be plugged in. The different variables are differentiated by their exponents in the equation.
Pm-1 = The feedback coefficient of the leftmost multiplier function in the register. The sequence Pm to P0 represents all multiplier functions, left to right. Because it multiplies the variable, if the feedback coefficient for a particular flip-flop is zero (no XOR gate), then that variable is nullified and removed from the polynomial. If the coefficient is one (XOR gate exists), then the variable remains. This is the intuitive genius of polynomial representation.
For example: The LFSR depicted in Rule 32 would be represented as x³ + x + 1.
Even if there weren't XOR gates in the entire LFSR, the equation would still be xm + 1, representing the ending and beginning points of feedback path.
Note that the number of variables in the polynomial does not represent the number of flip-flops - it represents the number of connections to the feedback path. For example, if there are 3 flip-flops in a register, then there are 4 possible connections, of which the leftmost and rightmost are guaranteed (as stated in the paragraph above). The other two connections are the ones with actual multiplier functions that decide whether they have an XOR gate, and thus whether they are a part of the polynomial. The variables absent from the polynomial give as much information as those included.
Depicted in the illustration below are the placements of the polynomial variables in relation to the feedback paths/connections they actually represent. Each middle flip-flop is incorporated into the feedback path (and thus into the polynomial) with its own XOR gate. Any minor confusion over the previous explanations should be resolved by the image below.
An illustration of how each variable of an LFSR polynomial accounts for the feedback path connections of an LFSR. The depicted LFSR has three flip-flops and both possible XOR gates, meaning that the polynomial has every variable present.
There are patterns in LFSR polynomials that can be used to determine whether the LFSR has a maximum-length period or not: see Rule 38.
All that is needed to represent a LFSR mathematically (aside from the initialization vector) is the degree m (the number of flip-flops), and the feedback coefficients. These characteristics can be represented in polynomial form as so:
P(x) = xm + Pm-1 × xm-1 + ... + P1 × x + P0
m = The number of flip-flops.
x = The simple polynomial variable, nothing to be plugged in. The different variables are differentiated by their exponents in the equation.
Pm-1 = The feedback coefficient of the leftmost multiplier function in the register. The sequence Pm to P0 represents all multiplier functions, left to right. Because it multiplies the variable, if the feedback coefficient for a particular flip-flop is zero (no XOR gate), then that variable is nullified and removed from the polynomial. If the coefficient is one (XOR gate exists), then the variable remains. This is the intuitive genius of polynomial representation.
For example: The LFSR depicted in Rule 32 would be represented as x³ + x + 1.
Even if there weren't XOR gates in the entire LFSR, the equation would still be xm + 1, representing the ending and beginning points of feedback path.
Note that the number of variables in the polynomial does not represent the number of flip-flops - it represents the number of connections to the feedback path. For example, if there are 3 flip-flops in a register, then there are 4 possible connections, of which the leftmost and rightmost are guaranteed (as stated in the paragraph above). The other two connections are the ones with actual multiplier functions that decide whether they have an XOR gate, and thus whether they are a part of the polynomial. The variables absent from the polynomial give as much information as those included.
Depicted in the illustration below are the placements of the polynomial variables in relation to the feedback paths/connections they actually represent. Each middle flip-flop is incorporated into the feedback path (and thus into the polynomial) with its own XOR gate. Any minor confusion over the previous explanations should be resolved by the image below.
An illustration of how each variable of an LFSR polynomial accounts for the feedback path connections of an LFSR. The depicted LFSR has three flip-flops and both possible XOR gates, meaning that the polynomial has every variable present.
There are patterns in LFSR polynomials that can be used to determine whether the LFSR has a maximum-length period or not: see Rule 38.
#
C. Rule .
Deriving Maximum-Length Periods from LFSR Polynomials:
Only LFSRs with primitive polynomials (see definition) yield maximum-length sequences.
Below is a table showcasing an example primitive polynomial for each m value 2-128. Note that there are multitudes of primitive polynomials for any given m value, too many to produce a complete list. There are 6.92 × 10⁷ primitive polynomials for an LFSR of m 31.
In the table below, take the values as representing the degrees in reverse order: x^0 + x^1 + x^2, for example. This ensures the +1, a necessary component of any LFSR polynomial as explained in Rule 37.
A table showcasing an example primitive polynomial for each m value 2-128.
Only LFSRs with primitive polynomials (see definition) yield maximum-length sequences.
Below is a table showcasing an example primitive polynomial for each m value 2-128. Note that there are multitudes of primitive polynomials for any given m value, too many to produce a complete list. There are 6.92 × 10⁷ primitive polynomials for an LFSR of m 31.
In the table below, take the values as representing the degrees in reverse order: x^0 + x^1 + x^2, for example. This ensures the +1, a necessary component of any LFSR polynomial as explained in Rule 37.
A table showcasing an example primitive polynomial for each m value 2-128.
#
C. Rule .
HOW TO CRACK A LINEAR FEEDBACK SHIFT REGISTER (LFSR):
Linear Feedback Shift Register's have many attractive properties, such as relative randomness and extraordinary efficiency - 100 flip-flops, a miniscule amount of space in hardware, produces a period of 2¹⁰⁰ - 1, for example. However, it fails on the last hurdle towards cryptographically secure generation: unpredictability.
By its very nature, an LFSR is a PRNG, a deterministic means of producing a keystream, thus opening it up to many vulnerabilities that can be exploited. The main principle that must be acknowledged in attempting to 'break' or 'crack' any stream cipher that utilizes an LFSR is as follows:
If an attacker knows (at least) 2m output values of an LFSR, he can recover the entire LFSR configuration, and from there, the plaintext.
Oscar must have the following prerequisite knowledge in order to crack the LFSR: Oscar, as always, must know the complete ciphertext string. Furthermore, he must know the degree m of the LFSR, i.e. the number of flip-flops in the register. This is reasonable knowledge to assume in real life, since the specifications of most cryptographic algorithms (including the m value) are made freely available under Kerckhoffs' Principle (Rule 3). Most damningly, he must also know the first few plaintext characters: x0, ..., x2m - 1. Much in the same fashion as how the Linear Congruential Generator was cracked (see Rule 29), it can be assumed that the header information of the document supplies this plaintext, and thus it is still realistic for that amount of plaintext to be known to the attacker.
Given this knowledge, Oscar simply has to follow a 3-step process in order to recover the entire key:
i ∈ ℤ2m
Si ≡ (xi + yi) mod 2.
Since Oscar knows the first 2m bits of both the plaintext and ciphertext, he is able to recover the first 2m keystream bits of the LFSR, which is still not enough: the maximum possible period is 2m - 1, so there remain a considerable number of keystream bits that need to be recovered before a complete decryption of the plaintext is possible.
Sm ≡ (Sm-1 × Pm-1 + ... + S0 × P0) mod 2
Since Oscar conveniently knows the m value, the only unknowns in this equation are every single feedback coefficient. Thus, there are a total of m unknowns that need to be solved for. In order to solve for m unknowns, a system-of-equations type problem, with m equations, must be created:
Sm ≡ (Sm-1 × Pm-1 + ... + S0 × P0) mod 2
Sm+1 ≡ (Sm × Pm-1 + ... + S1 × P0) mod 2
.
.
.
S2m-1 ≡ (S2m-2 × Pm-1 + ... + Sm-1 × P0) mod 2
As was done for Linear Congruential Generators, each unknown can easily be solved for by Gaussian Elimination ([[[[[) or Matrix Inversion ([[[[[[[[).
He can determine the initial state using the output bits that are already known (using the Diagonal Rule, see Rule 31), and from there he will be able to compute the full keystream, S2m+1 and beyond.
With the keystream, Oscar will now, of course, be able to recover the full plaintext:
xi ≡ (yi + si) mod 2
Linear Feedback Shift Register's have many attractive properties, such as relative randomness and extraordinary efficiency - 100 flip-flops, a miniscule amount of space in hardware, produces a period of 2¹⁰⁰ - 1, for example. However, it fails on the last hurdle towards cryptographically secure generation: unpredictability.
By its very nature, an LFSR is a PRNG, a deterministic means of producing a keystream, thus opening it up to many vulnerabilities that can be exploited. The main principle that must be acknowledged in attempting to 'break' or 'crack' any stream cipher that utilizes an LFSR is as follows:
If an attacker knows (at least) 2m output values of an LFSR, he can recover the entire LFSR configuration, and from there, the plaintext.
Oscar must have the following prerequisite knowledge in order to crack the LFSR: Oscar, as always, must know the complete ciphertext string. Furthermore, he must know the degree m of the LFSR, i.e. the number of flip-flops in the register. This is reasonable knowledge to assume in real life, since the specifications of most cryptographic algorithms (including the m value) are made freely available under Kerckhoffs' Principle (Rule 3). Most damningly, he must also know the first few plaintext characters: x0, ..., x2m - 1. Much in the same fashion as how the Linear Congruential Generator was cracked (see Rule 29), it can be assumed that the header information of the document supplies this plaintext, and thus it is still realistic for that amount of plaintext to be known to the attacker.
Given this knowledge, Oscar simply has to follow a 3-step process in order to recover the entire key:
Step 1:
Utilizing the definition of the encryption function of a stream cipher (Rule 25), the keystream at position i can be isolated:i ∈ ℤ2m
Si ≡ (xi + yi) mod 2.
Since Oscar knows the first 2m bits of both the plaintext and ciphertext, he is able to recover the first 2m keystream bits of the LFSR, which is still not enough: the maximum possible period is 2m - 1, so there remain a considerable number of keystream bits that need to be recovered before a complete decryption of the plaintext is possible.
Step 2:
In order to discover the remaining bits, the feedback coefficients of the multiplier functions must be discovered. This is done using the generalized summation equation of the LFSR (Rule 33). Expanding out the summation will produce the following equation:Sm ≡ (Sm-1 × Pm-1 + ... + S0 × P0) mod 2
Since Oscar conveniently knows the m value, the only unknowns in this equation are every single feedback coefficient. Thus, there are a total of m unknowns that need to be solved for. In order to solve for m unknowns, a system-of-equations type problem, with m equations, must be created:
Sm ≡ (Sm-1 × Pm-1 + ... + S0 × P0) mod 2
Sm+1 ≡ (Sm × Pm-1 + ... + S1 × P0) mod 2
.
.
.
S2m-1 ≡ (S2m-2 × Pm-1 + ... + Sm-1 × P0) mod 2
As was done for Linear Congruential Generators, each unknown can easily be solved for by Gaussian Elimination ([[[[[) or Matrix Inversion ([[[[[[[[).
Step 3:
Now that Oscar knows all of the Feedback Coefficients, he can build the LFSR himself.He can determine the initial state using the output bits that are already known (using the Diagonal Rule, see Rule 31), and from there he will be able to compute the full keystream, S2m+1 and beyond.
With the keystream, Oscar will now, of course, be able to recover the full plaintext:
xi ≡ (yi + si) mod 2
III.V Alternate Secure Stream Ciphers.
During the 1990s, stream ciphers were a center of attention for many cryptanalysts, who ruthlessly revealed vulnerabilites and weaknesses that opened particular popular ciphers of the time - this would fuel the predominance of block ciphers in modern cryptographic communications.
As a result, the eSTREAM project was established in 2004 by the "European Network of Excellence in Cryptology" (an E.U. front), which called for the development (and expert selection) of stream ciphers.
By 2008, several new, highly secure stream ciphers were developed, divided into two main categories/profiles:
1. Stream ciphers designed for implementation in software with high-volume data transfer requirements. Examples: Salsa20 (see Rule 40) & ChaCha (see Rule [[[[).
2. Stream ciphers designed for hardware implementation, with low power consumption, storage capabilities, and gate counts. Example: Trivium (see Rule [[[[).
# Add-Rotate-XOR (ARX) Ciphers: An algorithm in a cryptosystem that only uses additions, rotations, and XOR operations to generate its keystream.
# "Nonce": A number used only once.
#
C. Rule .
Salsa20:
Mathematical Definition:
[[[[[To be completed at a later date. I have determined this topic: "Salsa20", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
Explanation:
"Salsa20" is a family of profile-1 stream ciphers, developed in 2005. The PRNG utilizes a 32-bit ARX framework, with additional layers of security added through increased 'rounds' of encryption: the base cipher (Salsa20/20) uses 20 ciphers, while reduced-round, faster varients use 12 rounds (Salsa20/12) and 8 rounds (Salsa20/8), respectively.
Salsa20/20 (hereafter referred to as "Salsa20") supports key-lengths of either 128 or 256 bits, though 256 is recommended.
[[[[[To be completed at a later date. I have determined this topic: "Salsa20", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
Mathematical Definition:
[[[[[To be completed at a later date. I have determined this topic: "Salsa20", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
Explanation:
"Salsa20" is a family of profile-1 stream ciphers, developed in 2005. The PRNG utilizes a 32-bit ARX framework, with additional layers of security added through increased 'rounds' of encryption: the base cipher (Salsa20/20) uses 20 ciphers, while reduced-round, faster varients use 12 rounds (Salsa20/12) and 8 rounds (Salsa20/8), respectively.
Salsa20/20 (hereafter referred to as "Salsa20") supports key-lengths of either 128 or 256 bits, though 256 is recommended.
[[[[[To be completed at a later date. I have determined this topic: "Salsa20", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
#
C. Rule .
[[[[[Reserved for Future Usage. If additional rules are needed, then the WoO system will be used.[[[[[
[[[[[To be completed at a later date. I have determined this topic: "Salsa20, ChaCha, and Trivium", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
[[[[[To be completed at a later date. I have determined this topic: "Salsa20, ChaCha, and Trivium", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
#
C. Rule .
[[[[[Reserved for Future Usage. If additional rules are needed, then the WoO system will be used.[[[[[
[[[[[To be completed at a later date. I have determined this topic: "Salsa20, ChaCha, and Trivium", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
[[[[[To be completed at a later date. I have determined this topic: "Salsa20, ChaCha, and Trivium", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
#
C. Rule .
[[[[[Reserved for Future Usage. If additional rules are needed, then the WoO system will be used.[[[[[
[[[[[To be completed at a later date. I have determined this topic: "Salsa20, ChaCha, and Trivium", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[
[[[[[To be completed at a later date. I have determined this topic: "Salsa20, ChaCha, and Trivium", to be non-essential to the learning and understanding of the major fundamentals of Cryptography, and so it has been placed in the low-priority learning register.[[[[[

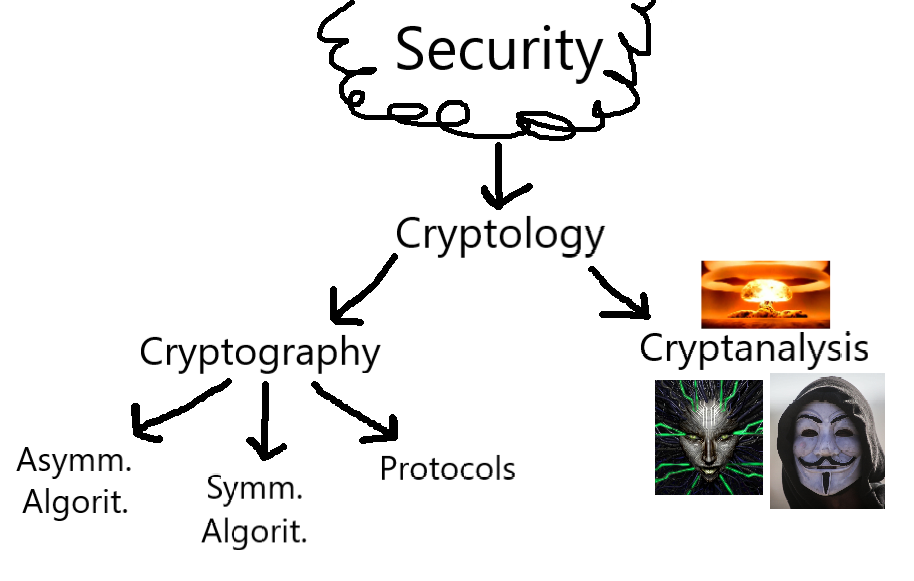
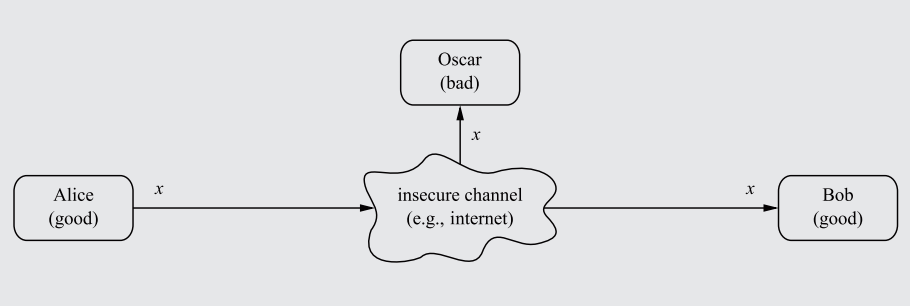
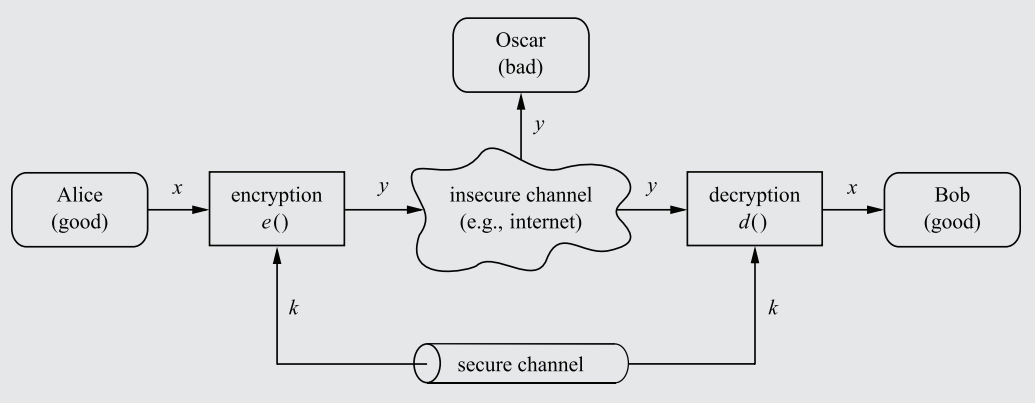
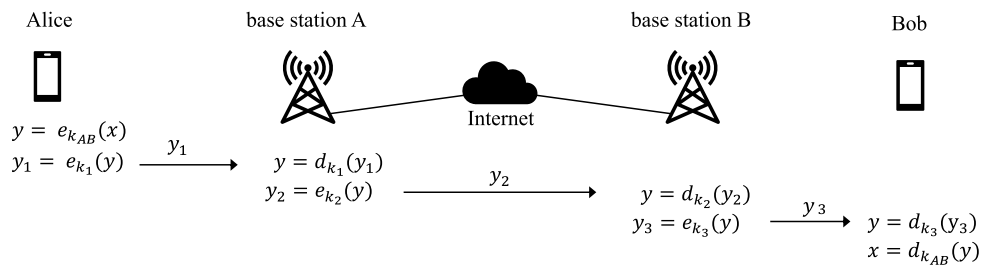
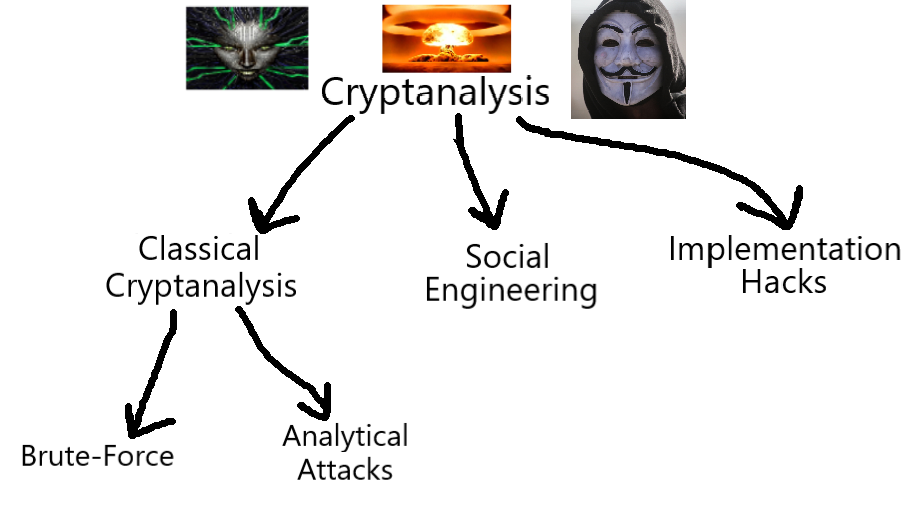

.png)